A liquid having area of free surface A and has an orifice at a depth of h with an area a, below the liquid surface, then find the velocity v of flow through the orifice
v=√2gh
v=√2gh√A2A2−a2
v=√2gh√AA−a
v=√2gh√A2−a2A2
Appliying Bernoulli's therorem,
pρ+12(v')2+gh=pρ+12v2+0
wher v' is velocity of all surface of liquid and v is velocity of efflux.
From equations of continuity
Av'av⇒v'=avA
12(avA)2+gh=12v2
v=√2gh√A2−a2A2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - BITSAT GUIDECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - All Questions
33 Videos
- GAUSS LAW AND ELECTRIC POTENTIAL THEORYBOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES
4 Videos
Similar Questions
Why do solids have any number of free surfaces and gases have no free sufaces at all ? Also compare with liquids.
View SolutionA pump is designed as a horizontal cylinder with a piston of areal A and and outlet orifice of areal a arranged mear the cylinder axis. Find the velocity of out flow of the liquid from the pump if the piston moves with a constant velocity under the action of a constant force F. The density of the liquid is ρ.
View Solution
Knowledge Check
Molecules on the surface of the liquid have
Amaximum kinetic energyBminimum kinetic energyCmaximum potential energyDminimum potential energyThe potential energy per unit change in area of the liquid surface , is
Asurface energyBwork doneCsurface tensionDtotal energyThe work done to increase unit area of the liquid surface is equivalent to
Asuface tensionBpowerCpressureDviscosity
Which of the following liquids has of the liquid surface is equivalent to
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
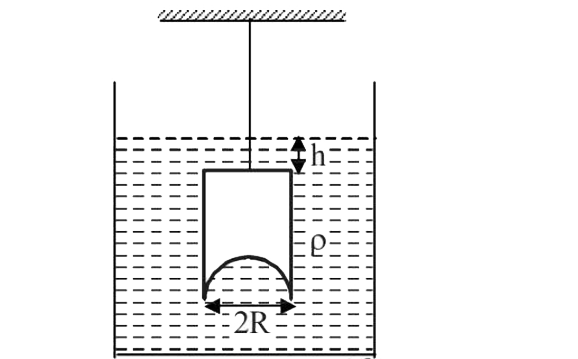
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View SolutionA tank of height 9.8 mis completely filled with water. It has an orifice at the centre of one vertical wall. What is the velocity of discharge (efflux) of water through the orifice ?
View SolutionA tank containing water has an orifice in one vertical side. If the centre of orifice is 4.9 m below the surface level in the tank, the velocity of discharge is:
View Solution
