A long chain of mass of mass M length L is being pulled with constant velocity on a rough incline with coefficient of friction μ. What rate frictional force on chain is increasing

310μMLgv
56μMLgv
zero
μMLgv
The correct Answer is:A
In a small time let dx length crossing from lower incline to upper incline
df=μM(dx)Lgcos37∘−μMLdxcos60∘
df=μMLg(cos37−cos60∘)dx
dfdt=μMLg(45−12)dxdt=310μMLgv
Topper's Solved these Questions
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Multiple answer question
Explore 20 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions
Explore 6 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -IV
Explore 40 Videos
Similar Questions
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
View Solution
Knowledge Check
A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
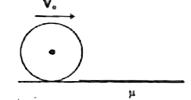 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208A uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
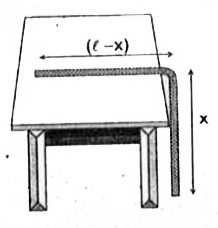 AL/3BL/2CL/4D2L/3
AL/3BL/2CL/4D2L/3A body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
Aθ=tan−1μBθ=tan−1(1μ)Cθ=tan−1(m)μDθ=tan−1(μ)m
A heavy chain with a mass per unite length p is pulled by the constant force F along a horizental surface consisting of a smooth section and a rough section. The chain is initially at rest on the rough surface with x=0 . If the coefficient of kinetic friction between the chain and the rough surface is μk determine the velocity v of the chain when x=L . The force F is hreater than μkogL in under to initate the motion ,

View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
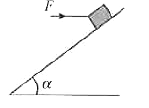
View SolutionA metal block of mass m is placed on a smooth metallic plane in support with string as shown in diagram. If after long time due to corrosiom, the contact surface becomes rough with coefficient of friction μ, then friction force acting on the block will be :
View SolutionA uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then

View SolutionIn the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is

View Solution

