A constant force (F) is applied on a stationary particle of mass 'm' The velocity attained by the particle in a certain displacement will be proportional to .
m
1/m
√m
1√m
The correct Answer is:D
To solve the problem, we need to determine how the velocity attained by a stationary particle of mass 'm' under the influence of a constant force 'F' is related to the displacement.
1. Identify the Given Information:
- A constant force F is applied to a stationary particle of mass m.
- The initial velocity u=0 (since the particle is stationary).
2. Use Newton's Second Law of Motion:
- According to Newton's second law, the acceleration a of the particle can be expressed as:
a=Fm
3. Apply the Kinematic Equation:
- We can use the kinematic equation that relates velocity, initial velocity, acceleration, and displacement:
v2=u2+2as
- Substituting u=0 and a=Fm:
v2=0+2(Fm)s
- This simplifies to:
v2=2Fsm
4. Solve for Velocity v:
- Taking the square root of both sides gives:
v=√2Fsm
5. Identify the Proportionality:
- From the equation v=√2Fsm, we can see that the velocity v is proportional to the square root of the displacement s when F and m are constants:
v∝√s
Conclusion:
The velocity attained by the particle in a certain displacement will be proportional to √s.
- A constant force F is applied to a stationary particle of mass m.
- The initial velocity u=0 (since the particle is stationary).
- According to Newton's second law, the acceleration a of the particle can be expressed as:
a=Fm
- We can use the kinematic equation that relates velocity, initial velocity, acceleration, and displacement:
v2=u2+2as
- Substituting u=0 and a=Fm:
v2=0+2(Fm)s
- This simplifies to:
v2=2Fsm
- Taking the square root of both sides gives:
v=√2Fsm
- From the equation v=√2Fsm, we can see that the velocity v is proportional to the square root of the displacement s when F and m are constants:
v∝√s
The velocity attained by the particle in a certain displacement will be proportional to √s.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -II (C.W)
Explore 71 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
A constant power P is applied on a particle of mass m. find kinetic energy, velocity and displacement of particle as function of time t.
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View Solution
Knowledge Check
A constant force (F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain interval of time will be proportional to
AmB1/mC√mD1√mA constant force F is applied to a body of mass m moving with initial velocity u. If after the body undergoes a displacement S its velocity becomes v, then the total work done is
Am[v2+u2]Bm2[u2+v2]Cm2[v2−u2]Dm[v2−u2]A force F=BeCt acts on a particle whose mass is m and whose velocity is 0 at t = 0. It's terminal velocity is :
ACmBBBmCCBCmD−BmC
A constant force of 2.50 N accelerates a stationary particle of mass 15 g through a displacement of 2.50 m. Find the work done and the average power delivered.
View SolutionThe value of force constant between the applied elastic force F and displacement will be
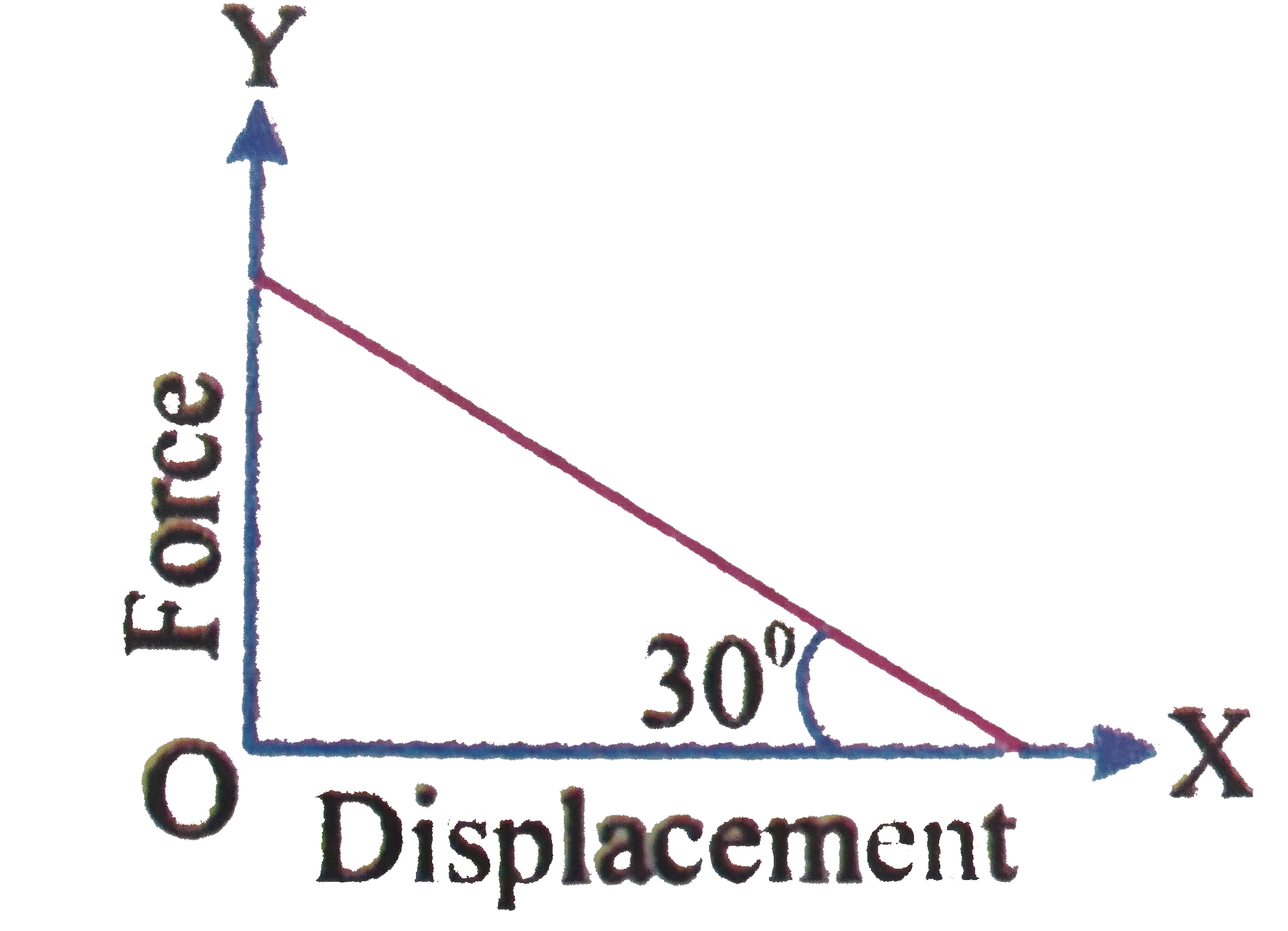
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionA particle of mass m1 moving with a velocity of 5 ms−1 collides head on with a stationary particle of mass m2. After collision both the particle move with a common velocity of 4ms−1then the value of m1/m2is :
View SolutionThe valve of force constant between the applied the applied elastic force F and displacement will be
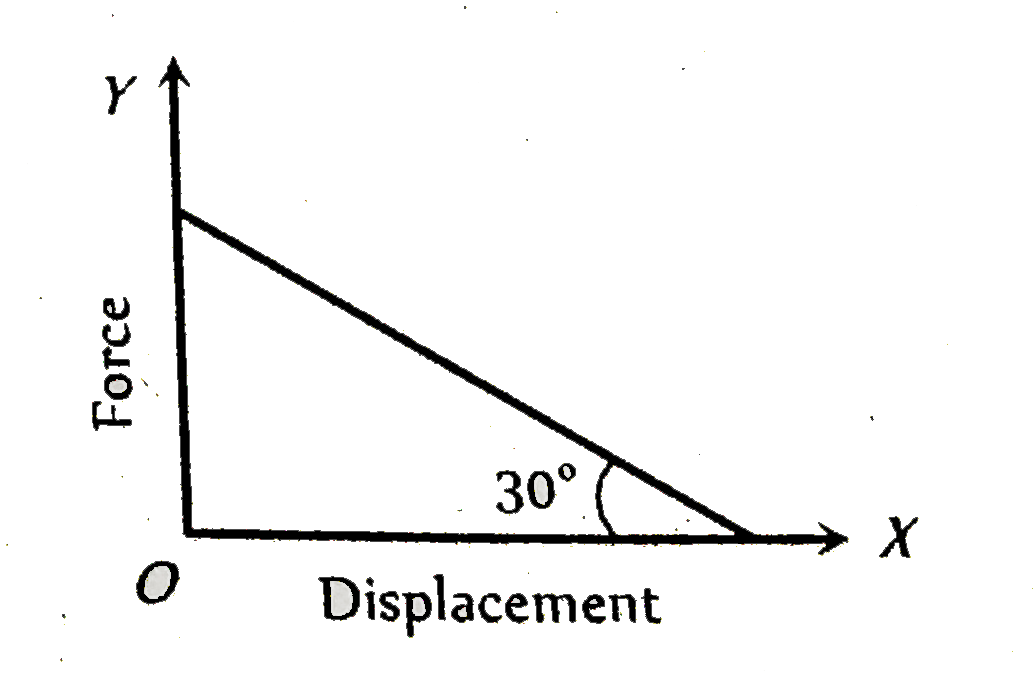
View Solution