Distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.

Let the gravitational field be zero at distance x from centre of star A. At P: Gravitational field due to A,
EA=GMx2 towards left.
Gravitational field due to B,
EB=G.16M(10a−x)2 towards right.
Since net gravitational field at P is zero i.e.,
EA=EB
GMx2=16M(10a−x)2
Taking square root
1x=4(10a−x)⇒x=2a
The body should be given velocity in such a manner so that on reaching at P, its velocity should be greater than zero. Total energy of body at the surface of B
=12mv2−G(16M)m2a−GM8a=12mv2−65GMm8a
Total energy of body at P
=12mv2P−G(16M)m(10a−x)−GMmx
12mv2P−16GMm8a−GMm2a
=12mv2P−5GMm8a
By conservation of energy
12mv2P−5GMm2a−12mv2−65GMm8a
12mv2P=12mv2−45GMm8a
v2P=v2−45GMm4a
vp≥0
v2−45GMm4a≥0
v≥√45GMm4a
vmin=√45GMm4a
Topper's Solved these Questions
Similar Questions
The distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii α and 2α. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of teh smaller star? Obtain the expression interms of G, M and α.
View SolutionDistance between the centres of two stars is 10a. The masses of these stars are M and 16M ans their radit a nd 2a respectively. A body of mass m is fired straight from the surface of the larger star tpwards the surface of the smaller star. What should be its minimum intial speed to reach the surface of the smaller star? Obtain the expression in terms of G, M and a.
View Solution
Knowledge Check
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the smaller star. The minimum initial speed for the body to reach the surface of smaller star is
A23√GmaB32√5GmaC23√5GmaD32√Gma
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.A√(59)GMaB√(49)GMaC√(39)GMaD√(29)GMaA particle is projected from the surface of one star towards other star of same radius a and mass with such a minimum velocity K√GMa, so that it is attracted towards other star. Find the value of K if two stars are 2r distance apart:
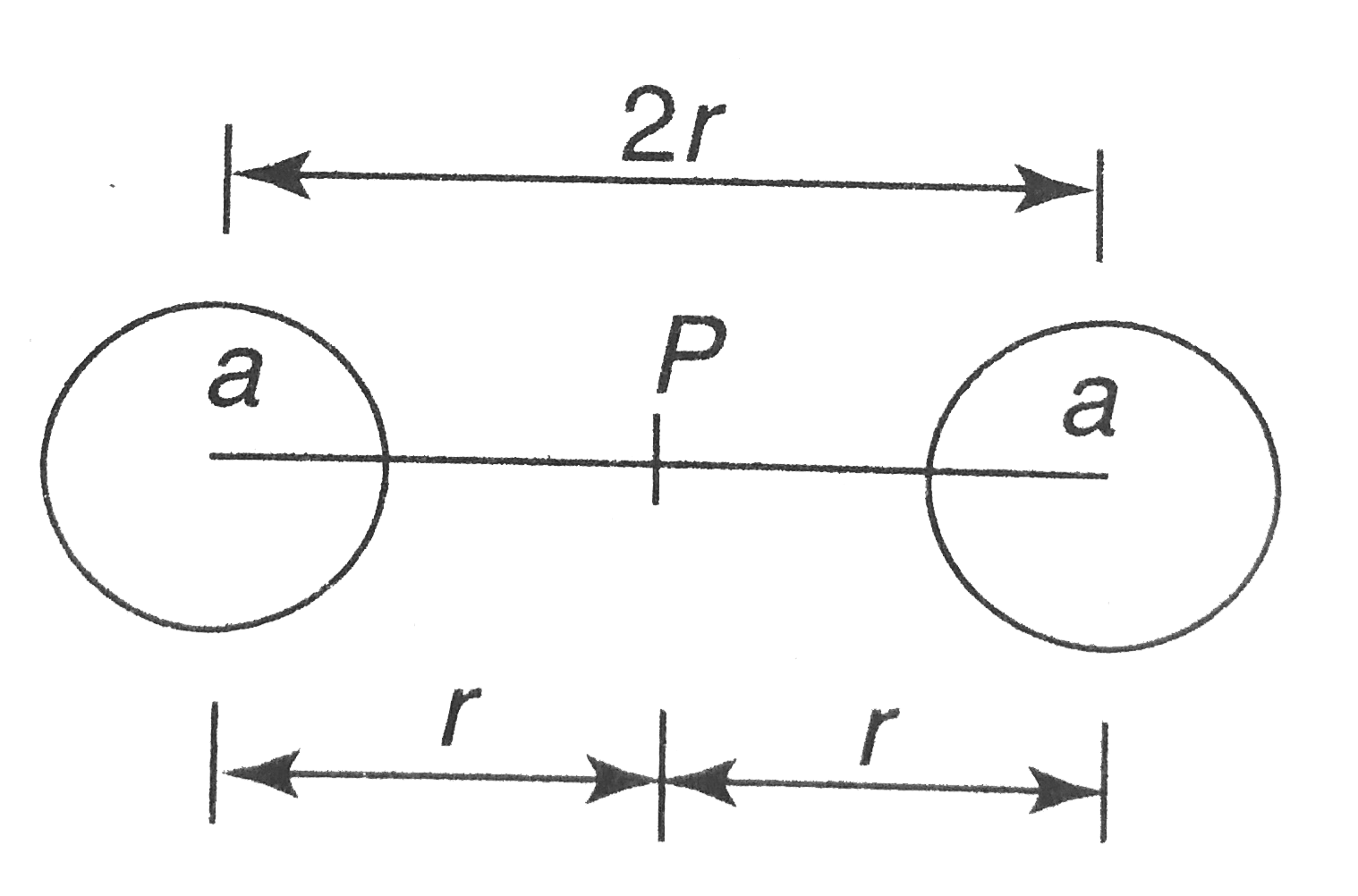 A2(r−a)[r(2r−a)]1/2B2(r−a)[r(r−a)]1/2Cr−a[r(r−a)]1/2Dr+a[r(r−a)]1/2
A2(r−a)[r(2r−a)]1/2B2(r−a)[r(r−a)]1/2Cr−a[r(r−a)]1/2Dr+a[r(r−a)]1/2
Distance between the centres of two rings is a. The masses of these rings are M and 4M. A body of mass m is fired straight from the centre of the heavier ring. What should be its minimum initial speed to cross of lighter ring ? The radius of the both ring is R. (Assume a>>R).

View SolutionTwo stars of masses M and 4M have radii x and 3x respectively. The distance between centres of two stars is 12x. A body of mass m is fired from the surface of bigger sphere towards smaller sphere. Find the minimum initial speed (in terms of G, x, M) required to reach the surface of smaller star.
View SolutionTwo planets have masses M and 16 M and their radii are a and 2a, respectively. The separation between the centres of the planets is 10a. A body of mass m is fired trom the surface of the larger planet towards the samller planet along the line joining their centres. For the body to be able to reach at the surface of smaller planet, the minimum firing speed needed is :
View SolutionThe masses of two stars are m1 and m2, and their separation is l. Determine the period T of their revolution in circular orbits about a common centre.
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View Solution
