A body is projected vartically upwards from the bottom of a crater of moon of depth R100 where R is the radius of moon with a velocity equal to the escape velocity on the surface of moon. Calculate maximum height attained by the body formt eh surface of the moon.
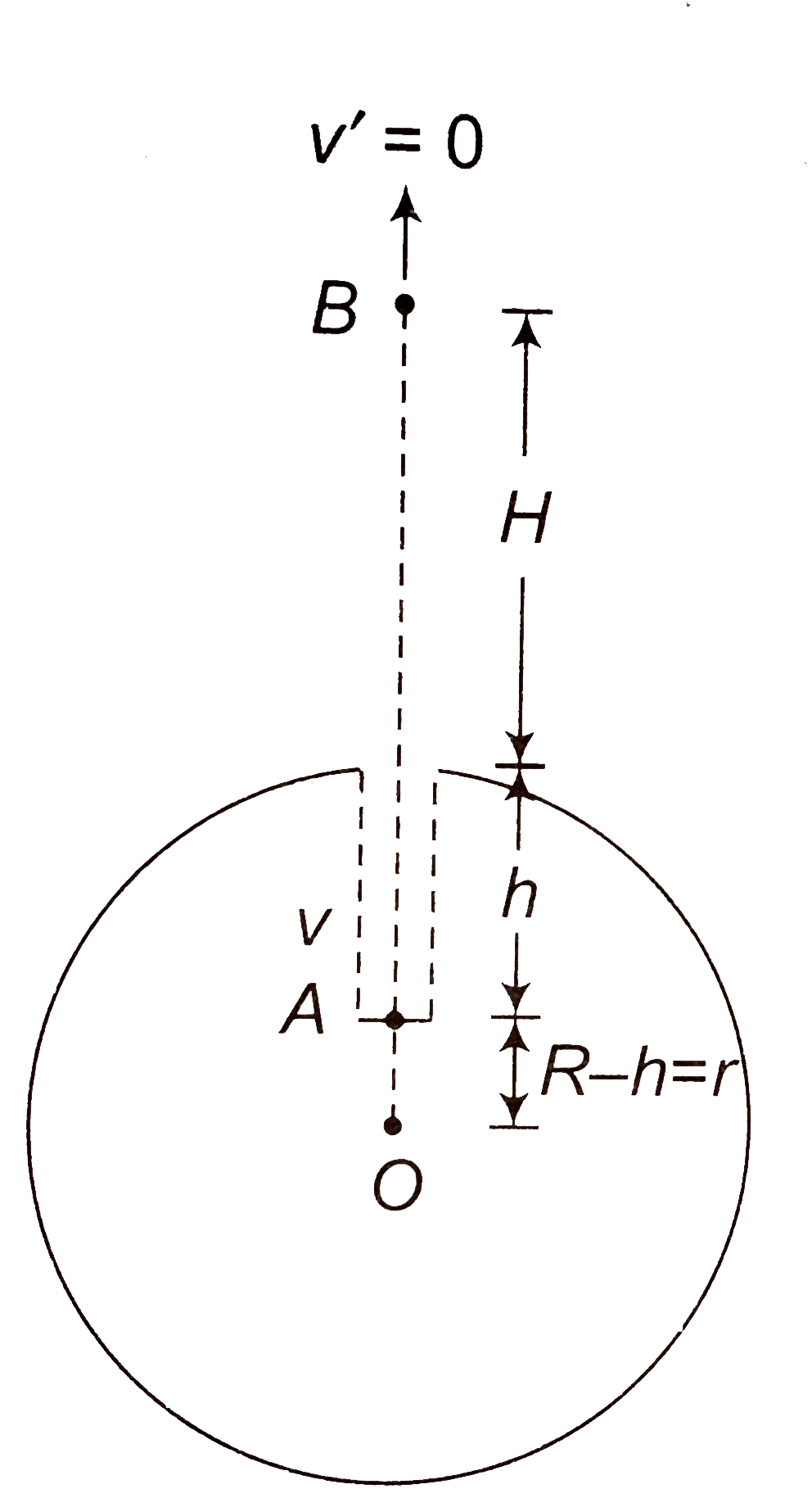
Gravitational potential inside solid sphere at distance r from centre.
V=−GM(3R2−r2)2R3
r=R−R100=99R100
Projection velocity at A,v=√2GMR
Applying energy conservation between A and B
KA+UA=KB+UB
KA+mVA=KB+VB
VA=−GM[3R2−(99R100)2]2R3=−GMR22R3[3−(0.99)2]
=−GM2R[3−(1−0.01)2]=−GM2R[3−(1−0.02)]
=−1.01GMR
vB=−GM(R+H)
KA=12mv2=12.2GMmR=GMmR
KB=0
GMmR−1.01GMR=0−GM(R+H)
−0.01=−11+HR
1+HR=100⇒H=99R
Topper's Solved these Questions
Similar Questions
A body is throw vertically upward with a velocity of 9.8 m/s. Calculate the maximum height attained by the body.
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View Solution
Knowledge Check
The escape velocity on the surface of the moon is small because_______
Athe moon's gravitational pull is smallBthe moon has no atmosphereCthe moon is not a planetDthe moon is revolving around the earth.If a body is to be projected vertically upwards from earth's surface to reach a height of 10R where R is the radius of earth. The velocity required to be si is
A√2411grB√2211grC√2011grD√1811grA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/4
A body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
View SolutionA body is projected horizontally from the surface of the earth (radius =R) with a velocity equal to n times the escape velocity. Neglect rotational effect of the earth. The maximum height attained by the body from the earth s surface is R/2. Then, n must be
View SolutionA body is projected up with a velocity equal to 3/4th of the escape velocity from the surface of the earth. The height it reaches is (Radius of the earth is R)
View SolutionThe escape velocity of a body from the surface of the earth is equal to
View Solution
