A small block of mass m is tied to the top of a smooth inclined plane with the help of a string of length L as shown in the figure. The inclined plane of inclination θ with horizontal is rotated with an angular velocity ω about a verticle axis passing through the end of the string fixed to the plane.
(a) Find the maximum value of ω so that the block maintains contact with the inclined plane.
(b) Find the ratio of the tension in the string and the normal reaction between the block and the plane.

We will solve this problem in rotating fram of reference by applying pseudo force. As the block is rest in this frame, hence the net force on each direction is zero.
r=Lcosθ
Resolving force ⊥ar to the plane and along the plane:
⊥ar to the plane:
N+mω2rsinθ−mgcosθ=0
N=mgcosθ−mω2rsinθ
For no loss of contact:
N≥0
mgcosθ−mω2rsinθ≥0
omeega≤√gcosθrsinθ=gcosθLcosθsinθ=gLsinθ
ωmax=√gLsinθ
Along the plane:
T−mgsinθ−mω2rcosθ=0
T=mgsinθ+mω2rcosθ
N=mgcosθ−mω2rsinθ
TN=gsinθ+ω2rcosθgcosθ−ω2rsinθ
=gsinθ+ω2Lcos2θgcosθ−ω2Lsinθcosθ

Topper's Solved these Questions
Similar Questions
A heavy block of length b and height h is placed at rest on a rough inclined plane of inclination θ with the horizontal, as shown in figure.

View SolutionFind total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .
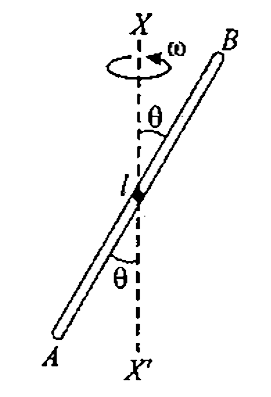
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθA sphere of weight W=100N is kept stationary on a rough inclined plane by a horizontal string AB as shown in figure. Then :
 Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3N
Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3N
A block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionA block of mass m is at rest on an incline having an angle of inclination θ with the horizontal. The incline is now being rotated with constant angular velocity ω about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as μ, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]
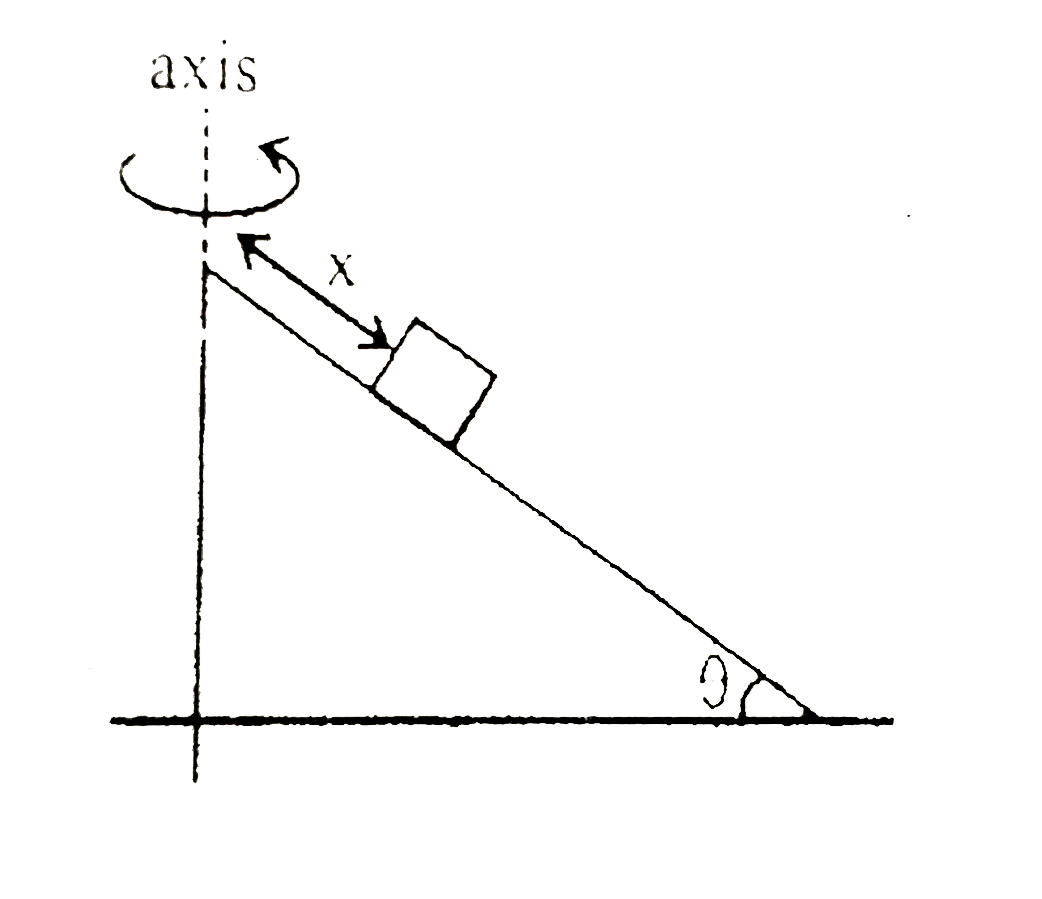
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform thin rod AB of mass M and length l attached to a string OA of length =12 is supported by a smooth horizontal plane and rotates with angular velocity ω around a vertical axis through O. A peg P is inserted in the plane in order that on striking it the rod will come to rest.
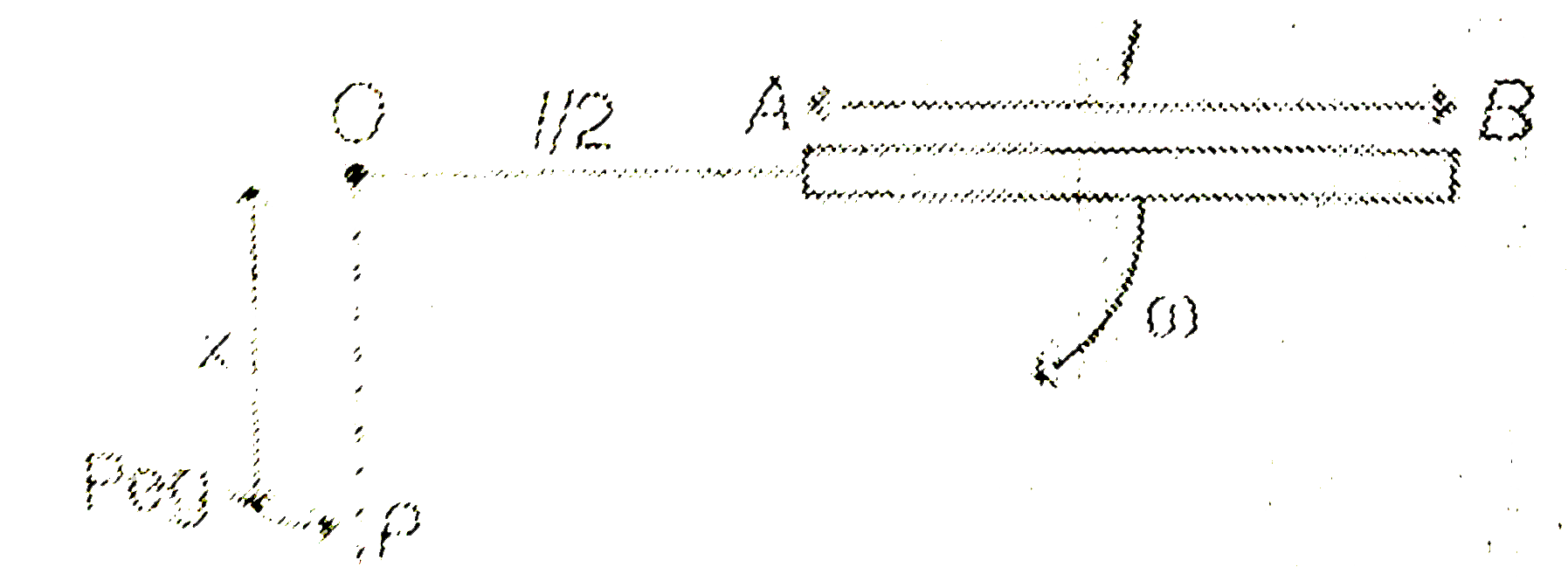
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
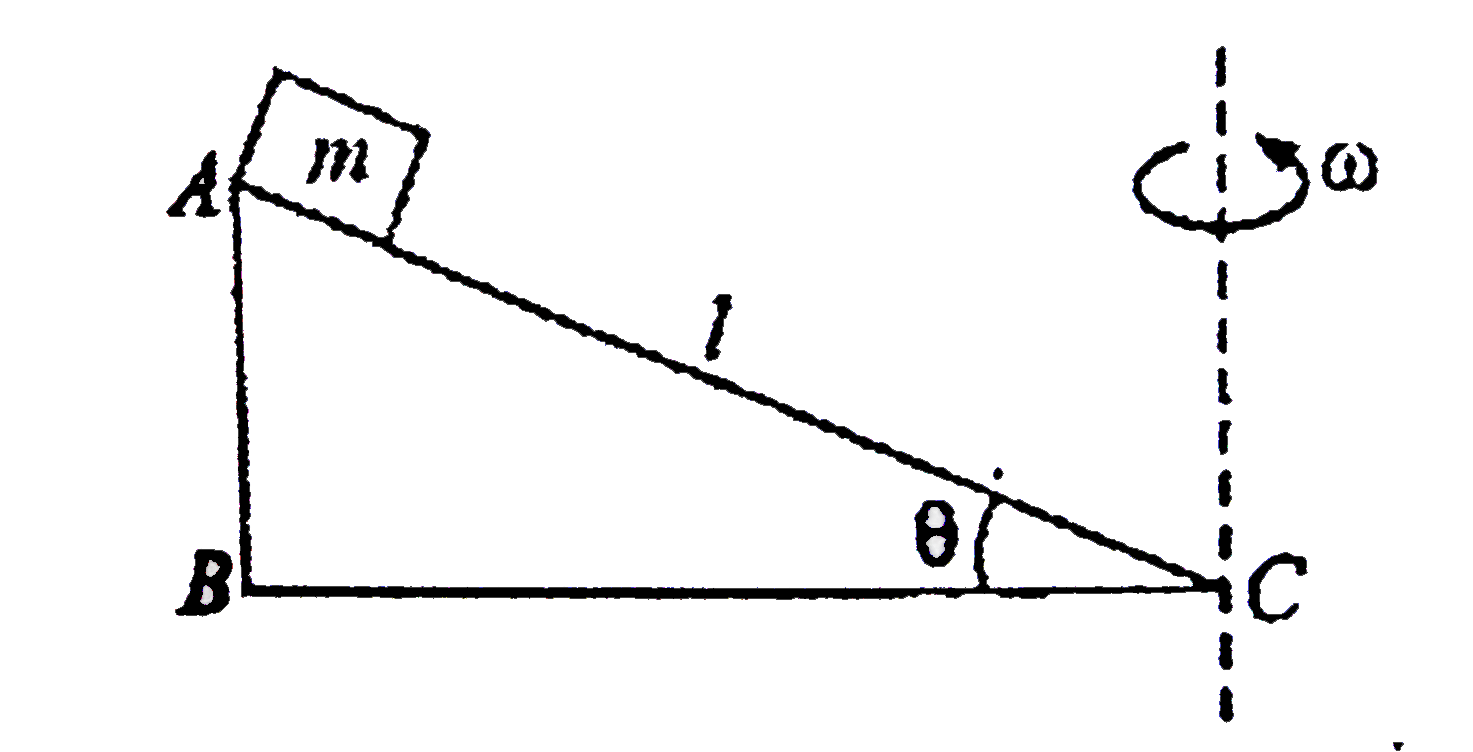
View Solution

