A block of mass m is at rest on an incline having an angle of inclination θ with the horizontal. The incline is now being rotated with constant angular velocity ω about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as μ, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]
![A block of mass m is at rest on an incline having an angle of inclination theta with the horizontal. The incline is now being rotated with constant angular velocity omega about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as mu, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_XI_RT_P8_E01_344_Q01.png)
gω2(μ+tanθ)(μtanθ−1)
gω2(μ−tanθ)(μtanθ+1)
gω2cosθ(μ−tanθ)(μtanθ+1)
gω2(μ−tanθ)(μtanθ−1)
The correct Answer is:C
N+mrω2sinθ=mgcosθ
mgsinθ+mrω2cosθ=Fdown

μ(mgcosθ−mrω2sinθ)=Fup
Fdown=Fup
r=g(μcosθ−sinθ)ω2(μsinθ+cosθ)
xcosθ=r
x=rcosθ=gω2cosθ(μcosθ−sinθ)(μsinθ+cosθ)
=gω2cosθ(μ−tanθ)(μtanθ+1)
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART B
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICA PART A
Explore 12 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (C )
Explore 15 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A heavy block of length b and height h is placed at rest on a rough inclined plane of inclination θ with the horizontal, as shown in figure.

View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθA block of mass m rests on a fixed incline plane of inclination θ with horizontal Assume friction is large enough to make the block stationary. Then choose correct alternative (s)
AMaximum value of horizontal component of friction is mgBangle θ at which horizontal component of friction is maximum is π4CMaximum value of horizontal component of friction is mg2DAngle θ at which horizontal component of friction is maximum is π3A block mass 'm' is placed on a frictionless inclined plane of inclination θ with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
AmgsinθBmgcosθCmgDnone of these
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
View SolutionThe coefficient of friction between the block and the inclined plane is μ.
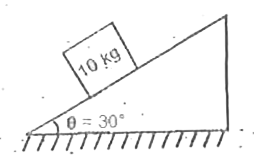
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
View Solution
