Consider the situation as shown in the figure. A rod of length L=2/27m pivodated near an end which is made to rotate in a horizontal plane with a constant angular speed. A ball is suspended bu a string also of length 2/27m from the other end of the rod. if the string makes θ=53∘ with vertical, find the angular speed of rotation.

The ball moves in horizontal circle of radius (L+Lsinθ)
Tcosθ)mg …..(i)
Tsinθ=mω2r=mω2(L+Lsinθ) ….(ii)
Dividing (ii) by (i),we get
tanθ=ω2L(1+sinθ)g
ω=√gtanθL(1+sinθ)=
⎷gtan53∘227(1+sin53∘)
=
⎷10×43227(1+45)=
⎷403227×95=10rad/s

Topper's Solved these Questions
Similar Questions
A rod of length L is pivoted at one end and is rotated with as uniform angular velocity in a horizontal plane. Let T1andT2 be the tensions at the points L//4 and 3L//4 away from the pivoted ends.
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View Solution
Knowledge Check
Figure shows as rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball of mass m is spuspended by a string angular also of length 20 cm from the other end of the rod. If the angle θ made by the stirng with the vertical is 300. find the anglular speed of the rotation. Take g=10m/s2
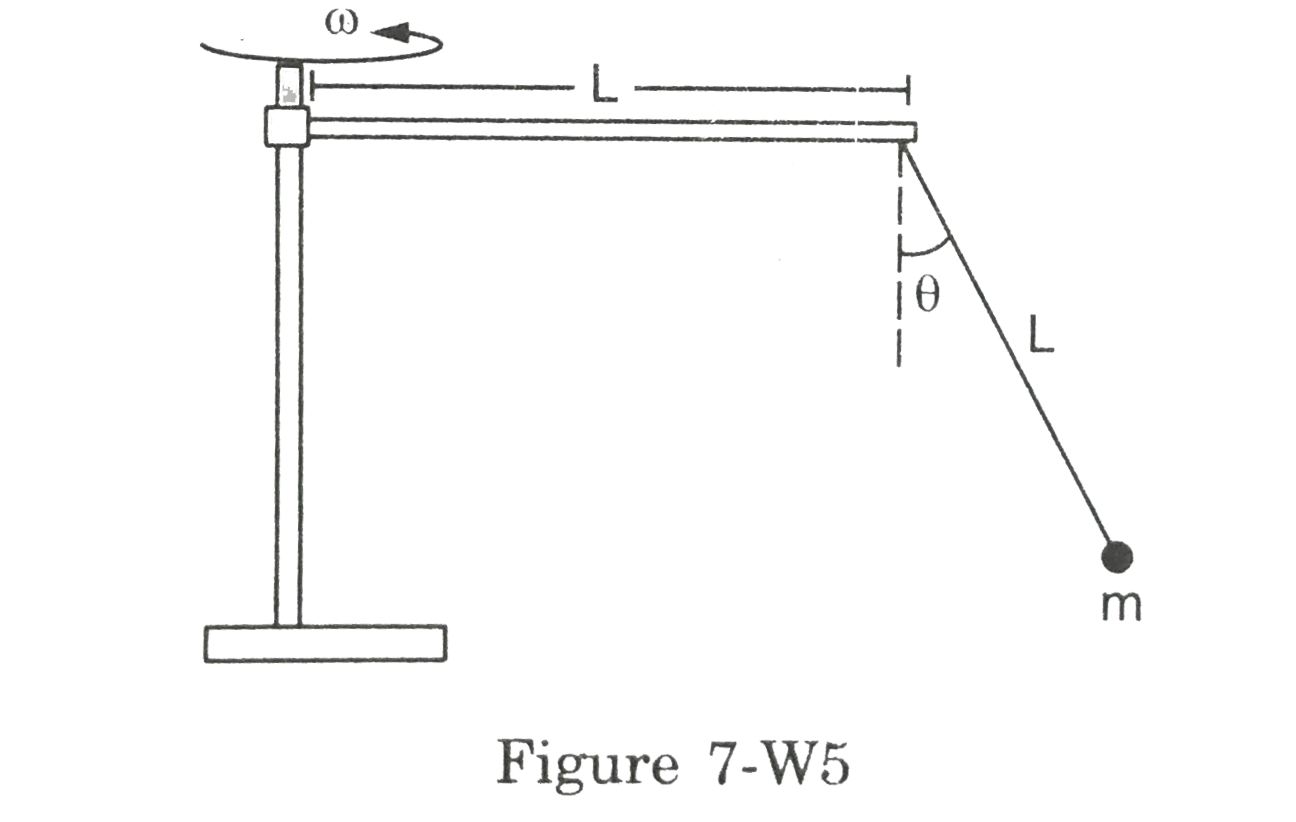 Aω=5.0rad/sBω=9.8rad/sCω=2.2rad/sDω=4.4rad/s
Aω=5.0rad/sBω=9.8rad/sCω=2.2rad/sDω=4.4rad/sConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
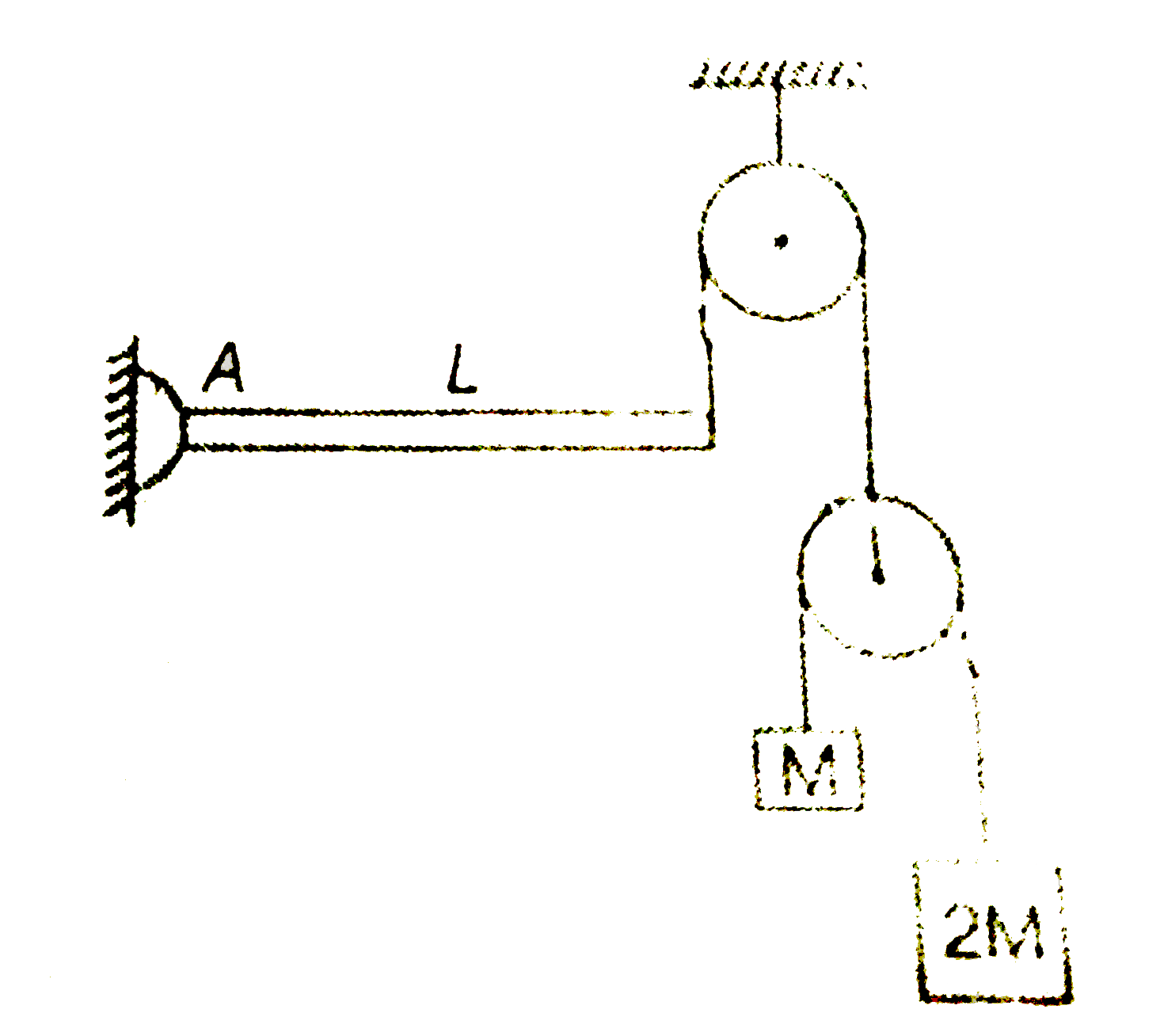 A43MB83MC163MD323M
A43MB83MC163MD323MA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
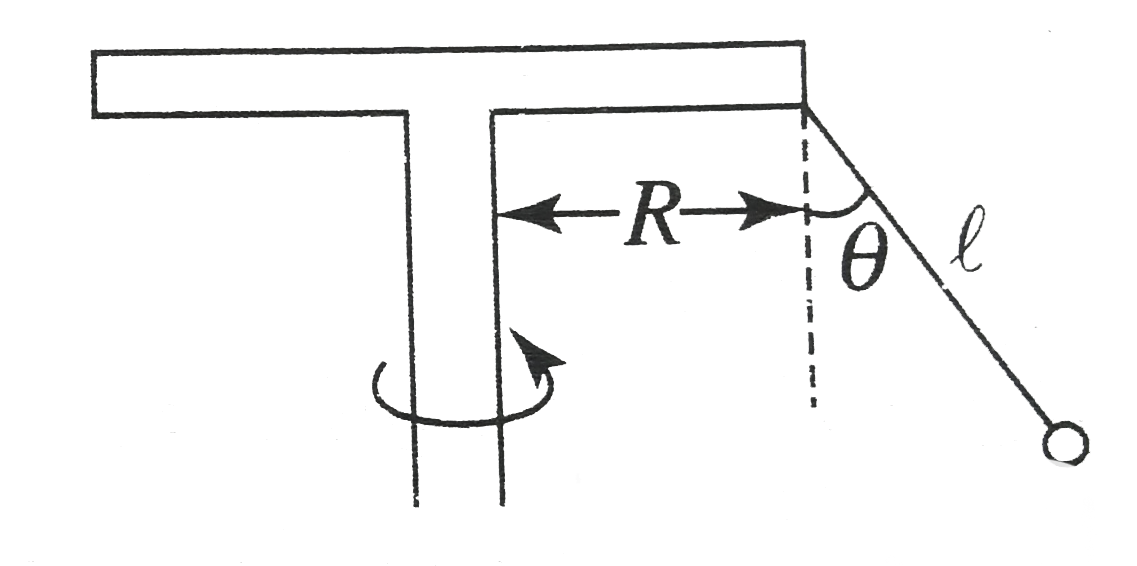 Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ
Aω=√>anθR+lsinθBω=√>anθR+<anθCω=√gcotθR+lsinθDω=√>anθR+lcosθ
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
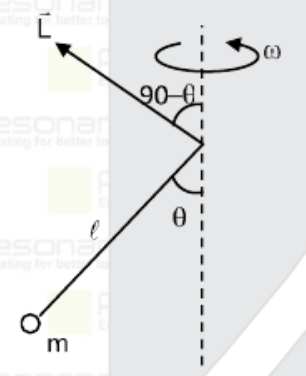
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform disc of radius 'R' is rotating about vertical axis passing through the centre in horizontal plane with constant angular speed. A massless pole AB is fixed on its circumference as shown in the figure. A light string of length 2R is tied at A and a small bob at its other end. In equilibrium string makes an angle 37∘ with vertical. The angular speed of disc is (takeR=311m,g=10m/s2)

View SolutionA uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
View Solution

