A wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)

2kg−m2
1.36kg−m2
4kg−m2
8kg−m2

τ=I0α
40×0.4=[I+4×(0.4)2](8)
I+0.64=2
I==1.36kgm2
Topper's Solved these Questions
Similar Questions
A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A stirng is wrapped over its rim and is ulle dby a force of 5.0 N. It is found that the torque roduces an angular acceleration 2.0 rads2 in the wheel. Calculate the moment of inertia of the wheel.
 View Solution
View SolutionA wheel of radius 20 cm and moment of inertia 1 kgm2 can rotate about its centre.A string is wrapped over its rim and is pulled by a force 'F' tangential to the rim of wheel.If angular acceleration produced is 2 rad/ s2 then the value of force 'F' is
View Solution
Knowledge Check
- Question 1 - Select One
A constant torque of 3.14 N mis exerted on a pivoted wheel. If the angular acceleration of the wheel is 4πrad/s2 then the moment of inertia of the wheel is
A0.25kgm2B2.5kgm2C4.5kgm2D25kgm2 - Question 2 - Select One
8 kg wheel has radius of gyration (1/4) m. The torque required to give it an angular acceleration of 4 rad/s2, is
A23NmB2 NmC32NmD3 Nm - Question 3 - Select One
A fly wheel of 0.4kg(m−2) M.I. and of 0.2 m radius can rotate about its axis. A rope is wrapped around its circumference and pulled with 10 N force. The value of angular acceleration in radsec2will be?
A5B2C10D0.8
A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
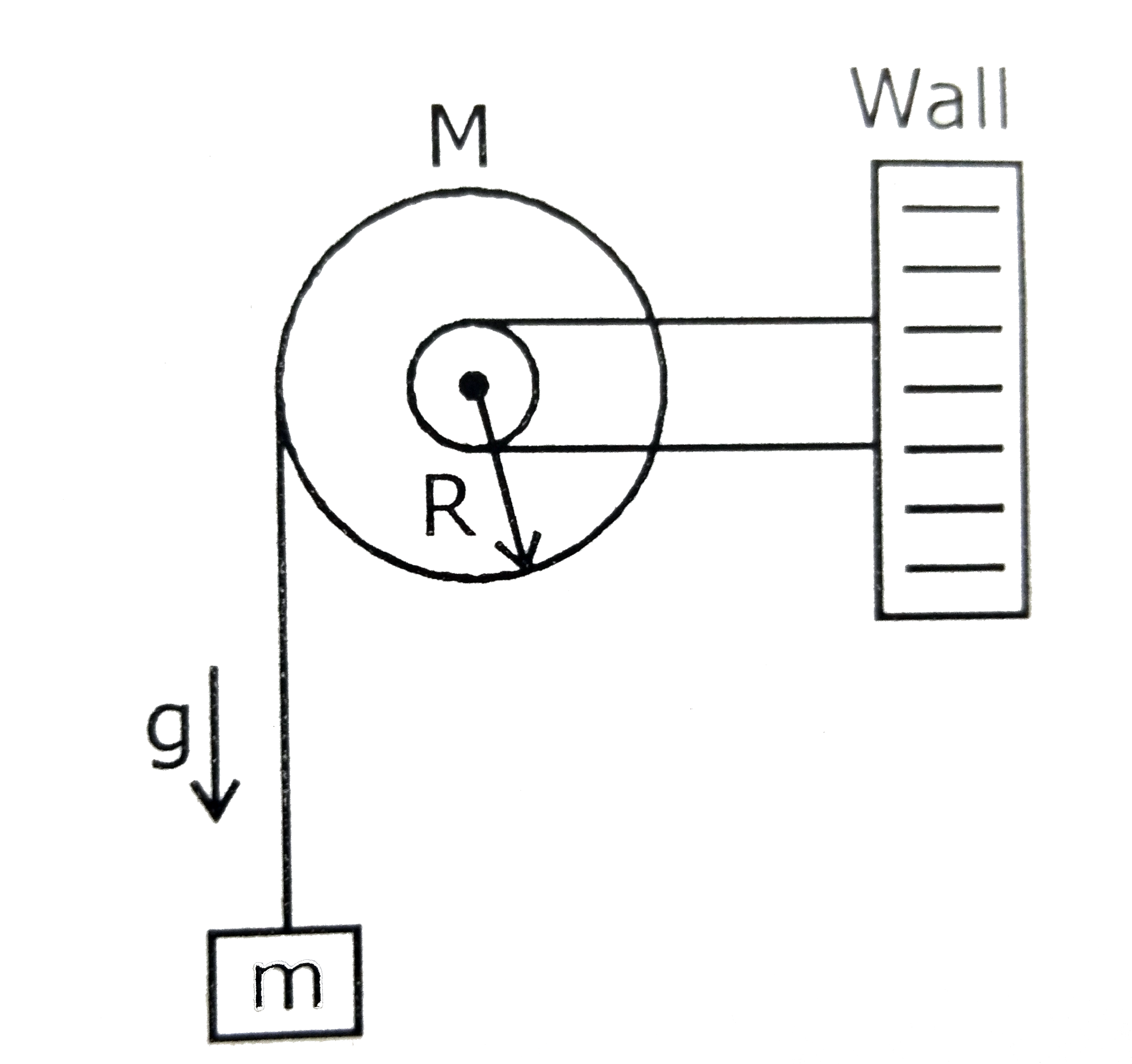 View Solution
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
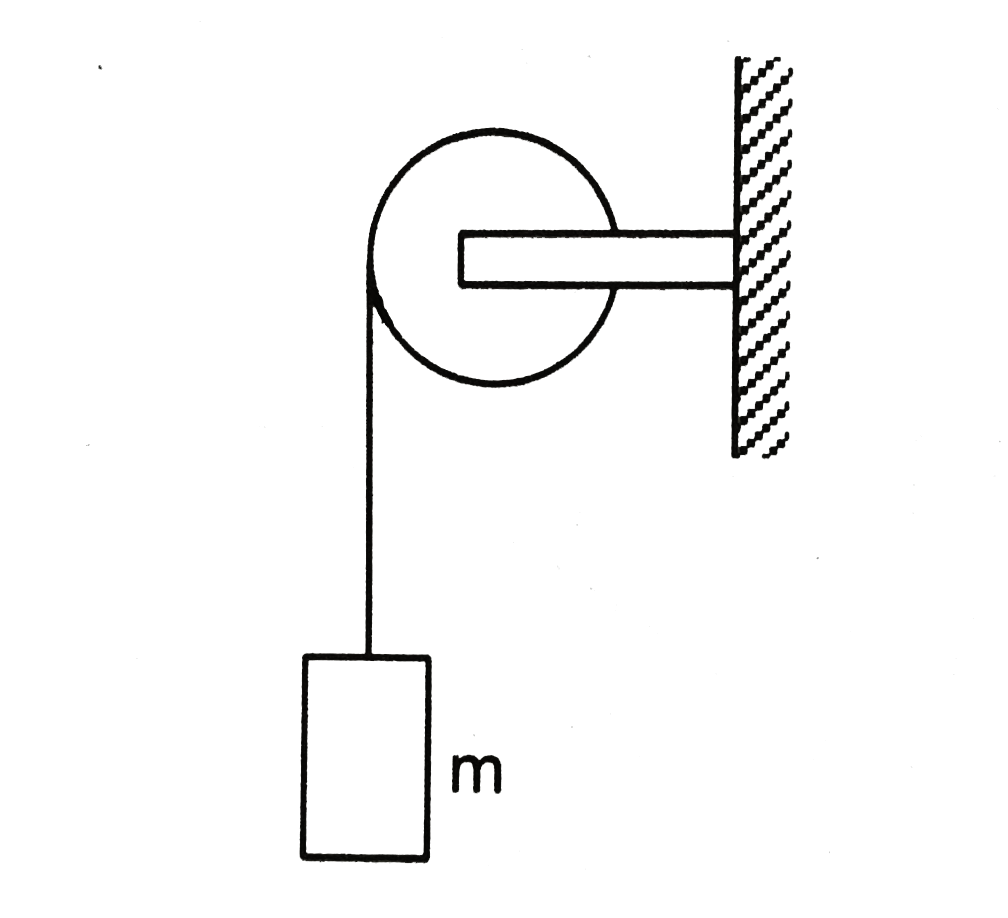 View Solution
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionThe moment of inertia of a flywheel is 4kgm2. What angular acceleration will be produced in it by applying a torque of 10 Nm on it?
View SolutionA stationary wheel starts rotating about its own axis at an angular acceleration 5.5rad/s2 . To acquire an angular velocity 420 revolutions per minute , the number of rotations made by the wheel is
View Solution

