For a system to be in equilibrium, the torques acting on it must balance. This is true only if the torques are taken about
the center of the system
the center of mass of the system
any point on the system
any point on the system or outside it.
To determine the conditions for equilibrium in a system, especially concerning torques, we can follow these steps:
1. Understanding Torque:
Torque (τ) is defined as the product of the force (F) and the distance (r) from the pivot point (or axis of rotation) to the point where the force is applied, multiplied by the sine of the angle (θ) between the force vector and the lever arm. Mathematically, it can be expressed as:
τ=r⋅F⋅sin(θ)
2. Condition for Equilibrium:
For a system to be in equilibrium, the net torque acting on it must be zero. This means that the sum of all torques about any point must equal zero:
∑τ=0
3. Choosing the Point of Reference:
The point about which torques are calculated can be any point in the system. It can be a point on the object or a point outside the object. The crucial aspect is that the sum of the torques about that point must be zero for the system to be in equilibrium.
4. Generalization of Equilibrium:
If the system is in equilibrium about one point, it will be in equilibrium about any point. This is due to the fact that if the net torque is zero at one point, it implies that the forces and their respective distances from that point are balanced, which will hold true for any other point as well.
5. Conclusion:
Therefore, the answer to the question is that the torques must balance about any point in the system for it to be in equilibrium. This means that the torques can be taken about any arbitrary point, and as long as the sum of the torques is zero, the system will remain in equilibrium.
Final Answer:
For a system to be in equilibrium, the torques acting on it must balance about any point.
Torque (τ) is defined as the product of the force (F) and the distance (r) from the pivot point (or axis of rotation) to the point where the force is applied, multiplied by the sine of the angle (θ) between the force vector and the lever arm. Mathematically, it can be expressed as:
τ=r⋅F⋅sin(θ)
For a system to be in equilibrium, the net torque acting on it must be zero. This means that the sum of all torques about any point must equal zero:
∑τ=0
The point about which torques are calculated can be any point in the system. It can be a point on the object or a point outside the object. The crucial aspect is that the sum of the torques about that point must be zero for the system to be in equilibrium.
If the system is in equilibrium about one point, it will be in equilibrium about any point. This is due to the fact that if the net torque is zero at one point, it implies that the forces and their respective distances from that point are balanced, which will hold true for any other point as well.
Therefore, the answer to the question is that the torques must balance about any point in the system for it to be in equilibrium. This means that the torques can be taken about any arbitrary point, and as long as the sum of the torques is zero, the system will remain in equilibrium.
For a system to be in equilibrium, the torques acting on it must balance about any point.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A : For a body to be in rotational equilibrium the net torque acting on the body about any point is zero.
R : For net torque to be zero, net force should also be zero.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion,BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion,CIf Assertion is true statement but Reason is false,DIf both Assertion and Reason are false statements,Torque acting on a rotating body
Avector(planar)Bvector(axial)CscalarDtensorThe torque acting on the coil is maximum if it is suspended in
Aunifrom magnetic fieldBradial magnetic fieldCearths magnetic fieldDnone of these
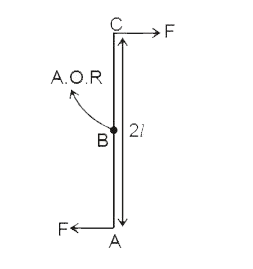
Write down torque about A, B, C
View SolutionThe torque acting on a body is the rotational analogue of
View SolutionIf the torque acting on a rigid body, under the application of a force, is zero then it's
View SolutionIf the torque acting on a rigid body, under the application of a force, is zero then it's
View SolutionIf torque acting upon a system is zero, the quantity that remains constant is
View Solution