The moment of inertia of a flywheel is 4kgm2. What angular acceleration will be produced in it by applying a torque of 10 Nm on it?
The correct Answer is:2.5rads−2
To find the angular acceleration produced in the flywheel when a torque is applied, we can use the relationship between torque (τ), moment of inertia (I), and angular acceleration (α). The formula is given by:
τ=Iα
Where:
- τ is the torque applied (in Nm),
- I is the moment of inertia (in kg m²),
- α is the angular acceleration (in rad/s²).
1. Identify the given values:
- Moment of inertia, I=4kg m2
- Torque applied, τ=10Nm
2. Use the formula for torque:
τ=Iα
Rearranging the formula to solve for angular acceleration α:
α=τI
3. Substitute the known values into the equation:
α=10Nm4kg m2
4. Calculate the angular acceleration:
α=104=2.5rad/s2
Final Answer:
The angular acceleration produced in the flywheel by applying a torque of 10 Nm is 2.5rad/s2.
---
- τ is the torque applied (in Nm),
- I is the moment of inertia (in kg m²),
- α is the angular acceleration (in rad/s²).
- Moment of inertia, I=4kg m2
- Torque applied, τ=10Nm
τ=Iα
Rearranging the formula to solve for angular acceleration α:
α=τI
α=10Nm4kg m2
α=104=2.5rad/s2
The angular acceleration produced in the flywheel by applying a torque of 10 Nm is 2.5rad/s2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem
24 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
The moment of inertia of a body is 2.5kgm2. Calculate the torque required to produce an angular acceleration of 18rads−2 in the body.
View SolutionThe moment of inertia of a wheel is 1000kg−m2. At a given instant, its angular velocity is 10rad/s. After the wheel rotates through an angle of 100 radians the wheel's angular velocity is 100rad/s. Find the torque applied on wheel.
View Solution
Knowledge Check
The moment of inertia of a flywheel having kinetic energy 360 J and angular speed of 20 rad/s is
A18 kg m2B1.8 kg m2C2.5 kg m2D9 kg m2A wheel whose moment of inertia is 2 kg m2 has an initial angular velocity of 50 rad/s. A constant torque of 10 Nm acts on the wheel. The time in which the wheel is accelerated to 80 rad's is
A12 sB3 sC6 sD9 sThe moment of inertia of a solid flywheel about its axis is 0.1kg−m2.A tangential force of 2 kg-wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration (in rad/sec2) of the mass :
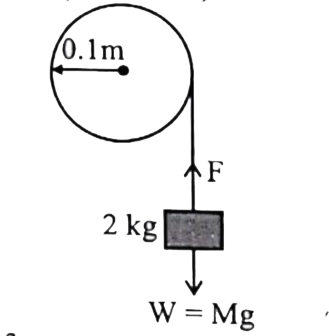 A163.3B16.3C81.66D8.16
A163.3B16.3C81.66D8.16
A flywheel having moment of inertia 20kgm2 rotates about its axis with an angular velocity of 100rads−1. If the moment of inertia of the flywheel is reduced to 10kgm2 without applying external torque, calculate the new angular velocity of the Flywheel.
View SolutionA wheel whose moment of inertia is 10kgm2 has an initial angular velocity of20rad/s. A constant torque of 20Nm acts on the wheel. The time in which wheel is acceleration to 100rad/s is
View SolutionA flywheel is rotating at an angular speed of 150 rpm. If the moment of inertia of the flywheel somehow decreases from 10kgm2 to 4kgm2, then what will be the new angular speed of the flywheel?
View SolutionA wheel of radius 0.4m can rotate freely about its axis as shown in the figure. A string is wrapped over its rim and a mass of 4kg is hung. An angular acceleration of 8rad/s2 is produced in it due to the torque. Then, the moment of inertia of the wheel is (g=10m/s2)

View SolutionA wheel of moment of inertia 2.5 kg m2 has an initial angular velocity of 40 rad s−1. A constant torque of 10 N m acts on the wheel. The time during which the wheel is accelerated to 60 rad s−1 is
View Solution
