A string is wound round the rim of a mounted flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel in rad/s2 is
50
25
12.5
6.25
To find the angular acceleration of the flywheel, we can follow these steps:
Step 1: Identify the given values
- Mass of the flywheel, m=20kg
- Radius of the flywheel, r=20cm=0.2m
- Tension in the string, T=25N
Step 2: Calculate the torque (τ)
The torque (τ) produced by the tension in the string is given by the formula:
τ=T×r
Substituting the values:
τ=25N×0.2m=5N m
Step 3: Calculate the moment of inertia (I)
For a solid disc (flywheel), the moment of inertia is given by:
I=12mr2
Substituting the values:
I=12×20kg×(0.2m)2=12×20×0.04=0.4kg m2
Step 4: Relate torque to angular acceleration (α)
According to Newton's second law for rotation:
τ=Iα
Substituting the values we have:
5N m=0.4kg m2×α
Step 5: Solve for angular acceleration (α)
Rearranging the equation to solve for α:
α=5N m0.4kg m2=12.5rad/s2
Final Answer
The angular acceleration of the flywheel is:
α=12.5rad/s2
---
- Mass of the flywheel, m=20kg
- Radius of the flywheel, r=20cm=0.2m
- Tension in the string, T=25N
The torque (τ) produced by the tension in the string is given by the formula:
τ=T×r
Substituting the values:
τ=25N×0.2m=5N m
For a solid disc (flywheel), the moment of inertia is given by:
I=12mr2
Substituting the values:
I=12×20kg×(0.2m)2=12×20×0.04=0.4kg m2
According to Newton's second law for rotation:
τ=Iα
Substituting the values we have:
5N m=0.4kg m2×α
Rearranging the equation to solve for α:
α=5N m0.4kg m2=12.5rad/s2
The angular acceleration of the flywheel is:
α=12.5rad/s2
Topper's Solved these Questions
Similar Questions
A cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
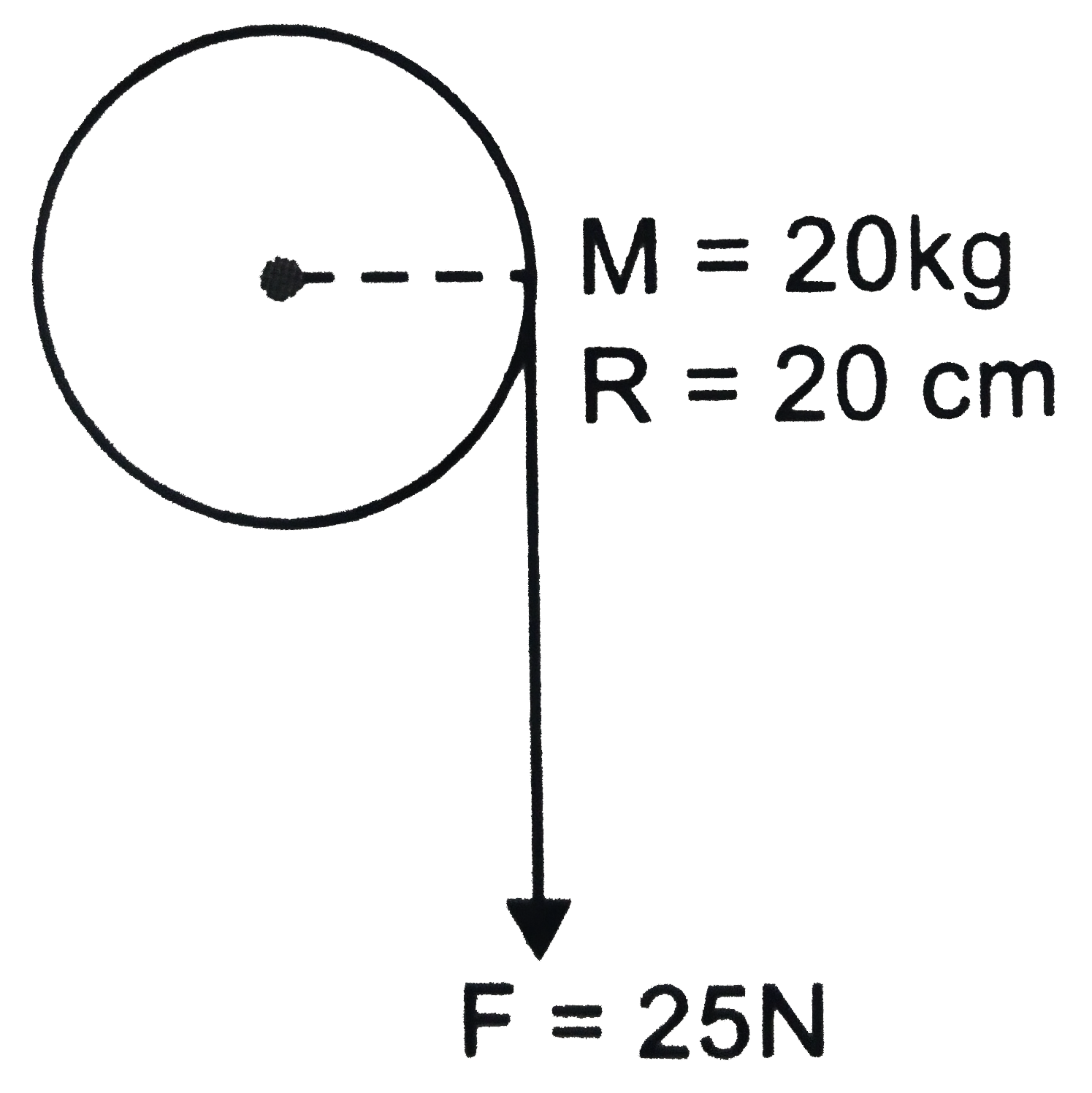
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of 2rad s−2 ?
View Solution
Knowledge Check
A cord of negligible mass is wound round the rin of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. The work done by the pull when 2 m of the cord is unwound is
A20 JB25 JC45 JD50 JA cord is wound over the rim of a flywheel of mass 20 kg and radius 25 cm. A mass 2.5 kg attached to the cord is allowed to fall under gravity. The angular acceleration of the flywheel is
A25rad/s2B20rad/s2C10rad/s2D5rad/s2A rope is wound round a hollow cylinder of mass 2 kg and radius 0.5 m. If the rope is pulled with a force of 80 N, the angular acceleration of the cylinder will be -
A20 rad/s2B40 rad/s2C60 rad/s2D80 rad/s2
A torque of 10 Nm is applied to a flywheel of mass 10 kg and radius of gyration 50 cm. What is the resulting angular acceleration ?
View SolutionA rope is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? What is the linear acceleration of the rope ?
View SolutionA body of mass 5kg is attached to a weightless string wound round a cylinder of mass 8kg and radius 0.3m. The body is allowed to fall. Calculate (i) tension in the string, (ii) acceleration with which the body falls and (iii) angular acceleration of the cylinder.
View SolutionA body of mass 5 kg is attached to a weightless string wound round a cylinder of mass 8 kg and radius 0.3 m. The body is allowed to fall. Calculate (i) tension in the string (ii) acceleration with which the body falls and (iii) the angular acceleration of the cylinder.
View SolutionA rope is wound round a hollow cylinder of mass 3kgandradius40cm. If the rope is pulled with a force of 30N, what is the angualr acceleration of the cylinder ?
View Solution
