The angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2r2. Then the angular acceleration of the body is
θ1
θ2
2θ1
2θ2
θ=θ0+θ1t+θ2t2,ω=dθdt=θ1+2θ2t
α=dωdt=2θ2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2t2. Then the angular acceleration of the body is
Aθ1Bθ2C2θ1D2θ2If angular velocity of a disc depends an angle rotated θ as ω=θ2+2θ, then its angular acceleration α at θ=1 rad is :
A8rad/s2B10rad/s2C12rad/s2DNone of theseAngular displacement (θ) of a flywheel varies with time as θ=at+bt2+ct3 then angular acceleration is given by
Aa+2bt−3ct2B2b−6tCa+2b−6tD2b+6ct
Angular displacement (θ) of a flywheel varies with time as θ=2t+3t2 radian. The angular acceleration at t=2s is given by
View SolutionA body cools in a surrounding which is at a constant temperature of θ0 Assume that it obeys Newton's law of cooling Its temperature θ is plotted against time t Tangents are drawn to the curve at the points P(θ=θ1) and Q(θ=θ2) These tangents meet the time axis at angle of ϕ2 andϕ1 as shown
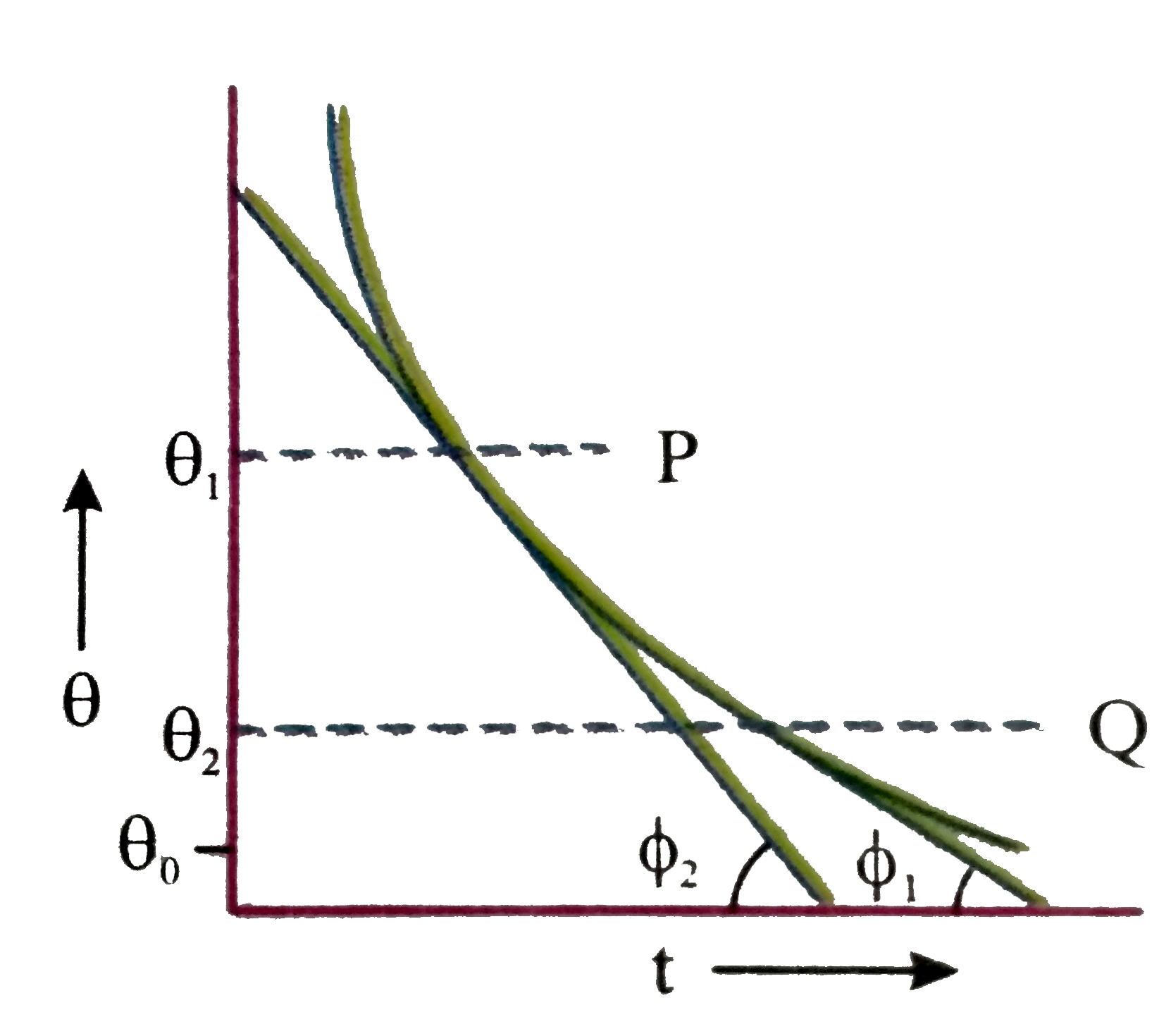 .
.
View SolutionThe angular displacement of a particle performing circular motion is
θ=t460−t4
where θ is radian and 't' is in seconds. Then the acceleration of a particle at the end of 10 s will be
View SolutionIf θ is an acute angle and tan2θ+1tan2θ=2 , then the value of θ is :
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newyon's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
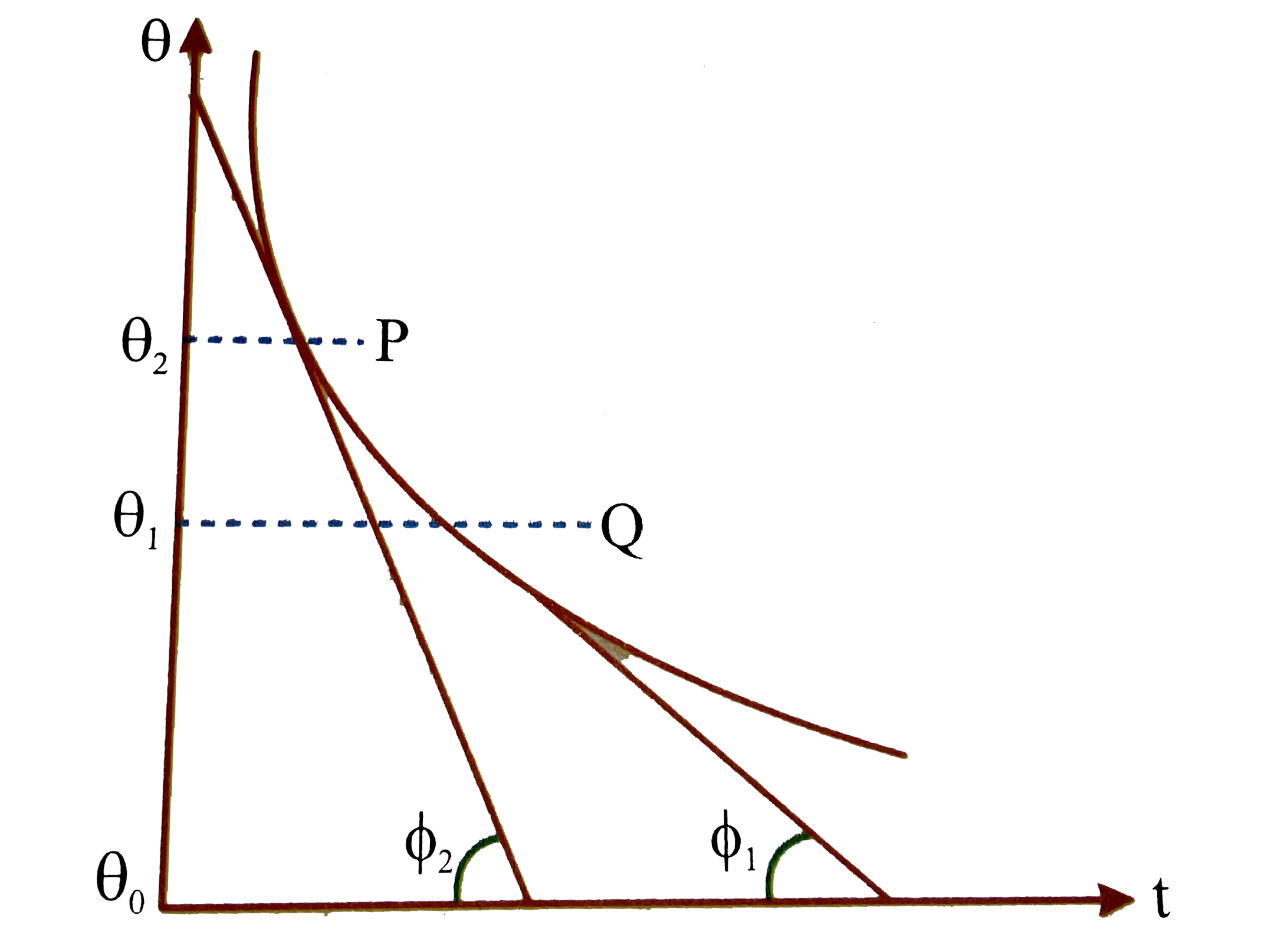
View Solution