A uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can be leaned without slipping.
Let the weight of ladder be W and length 2a.
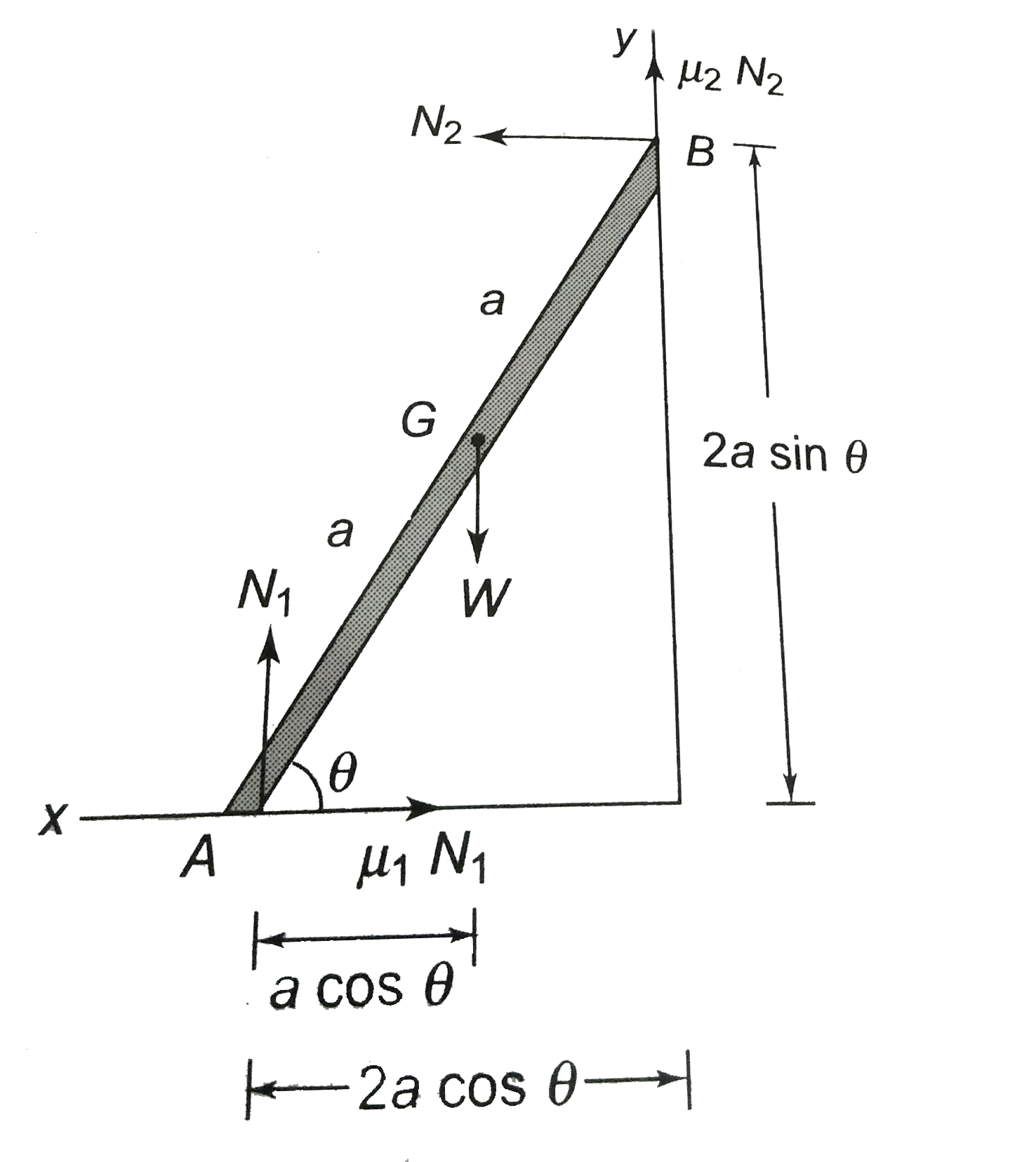
Since the ladder is in equilibrium
ΣFx=0⇒N2=μ1N1 .....(i)
ΣFy=0⇒N1+μ2N2=W ......(ii)
ΣτA=0
⇒W×acosθ=N2×2asinθ+μ2N2×2acosθ .......(iii)
From (i) and (ii), we have
N1=W1+μ1μ2,N2=μ1W1+μ1μ2in (iii)
Wcosθ=2μ1Wsinθ1+μ1μ2+2μ2μ1Wcosθ1+μ1μ2
2μ1sinθ1+μ1μ2=(1−2μ1μ21+μ1μ2)cosθ
tanθ=1−μ1μ22μ1
θ=tan−1(1−μ1μ22μ1)
Topper's Solved these Questions
Similar Questions
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
Knowledge Check
A uniform rod is made to lean between rough vertical wall and the ground. Friction coefficient between rod and walls is μ1=12 and between the rod and the ground is μ2=14. The rod is about to slip at contact surfaces. The correct options are:
 AThe normal reaction between rod and wall is μ2W1+μ1μ2BNormal reaction between rod and ground is W1+μ1μ2CN2>N1DN1>N2
AThe normal reaction between rod and wall is μ2W1+μ1μ2BNormal reaction between rod and ground is W1+μ1μ2CN2>N1DN1>N2A man is running on the ground .It is known that the coefficient of friction between the man and the ground is μ . Then which of the following statements is correct
ANormal reaction between man and ground is equal to weight of manBThe direction of friction on man is in the direction of normal reaction on the manCDirection of friction on man is opposite to the direction of motion of manDMaximum acceleration of man can be 2μgIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
 Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
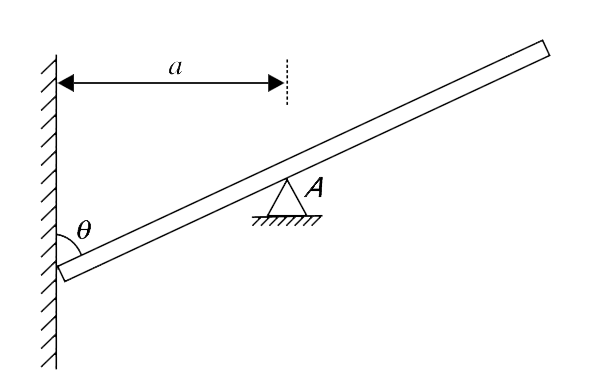
A uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
View SolutionA uniform ladder of length l rests against a smooth, vertical wall (figure). If the mass of the ladder is m and the the coefficient of static friction between the ladder and the ground is μs=0.375 and the minimum angle θmin at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
View SolutionA ladder rests on the floor of a room, leaning agains a wall. If the coefficient of static friction between the ladder the floor is μf and that between ladder and is μw, what is the minimum angle θ that the ladder can make with the floor if the ladder is not to slip? Assume that the mass of the ladder is distributed uniformly.

View SolutionA rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View SolutionA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
View Solution
