A particle A moves along a circle of radius R=50cm so that its radius vector r relative to the point O(figure) rotates with the constant angular velocity ω=0.40rad/s. Find the modulus of the velocity of the particle, and the modulus and direction of its total acceleration.

Video Solution
Text Solution
Angular velocity of A about the center of circle
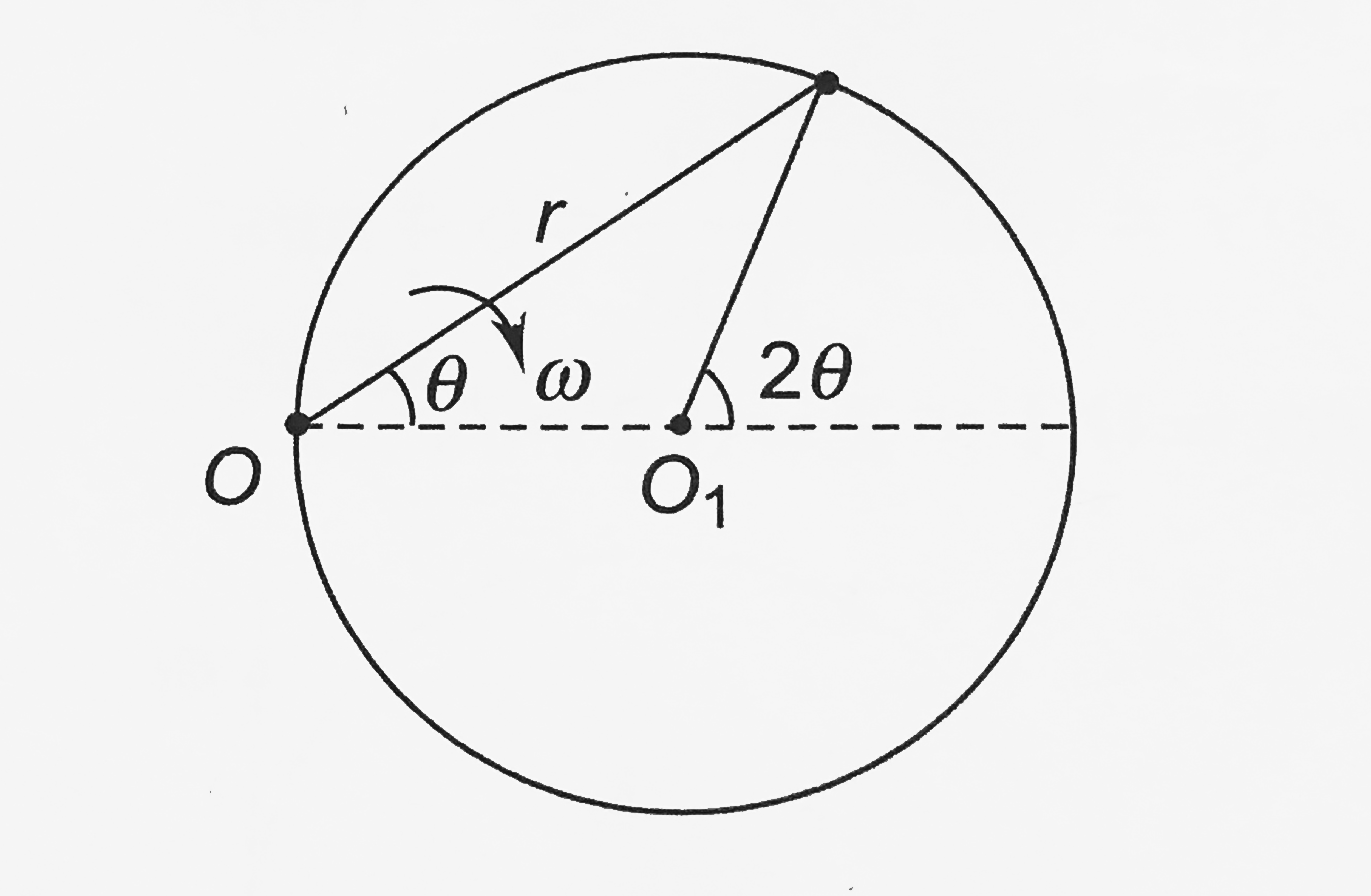
ωA=2ω
vA=ωAR=2ωR=2×0.4×0.5=0.4m/s
aA=ω2AR=4ω2R=4×(0.4)2×0.5=0.32m/s2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle 'A' moves along a circle of radius R = 50 cm, so that its radius vetor 'r' relative to the point O rotates with the constant angular velocity ω=0.4rad/s. Then :
Alinear velocity of particle is 0.2m/sBlinear velocity of particle is 0.4m/sCmagnitude of net acceleration is 0.08m/s2Dacceleration of particle is zeroA particle moves along a circle of radius R =1m so that its radius vector →r relative to a point on its circumference rotates with the constant angular velocity ω=2rad/s. The linear speed of the particle is
A4m/sB2m/sC1m/sD0.5m/sA particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
AπRBRC2πRD2R
A particle moves with constant angular velocity in a circle. During the motion its
View SolutionA particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
View SolutionA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View Solution
