Question

In figure, the stiffness of the spring is $k$ and mass of the block is $m$. The pulley is fixed. Initially, the block $m$ is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block $m$. Neglect the mass of the spring and that of the string. Also neglect the friction.

Explanation

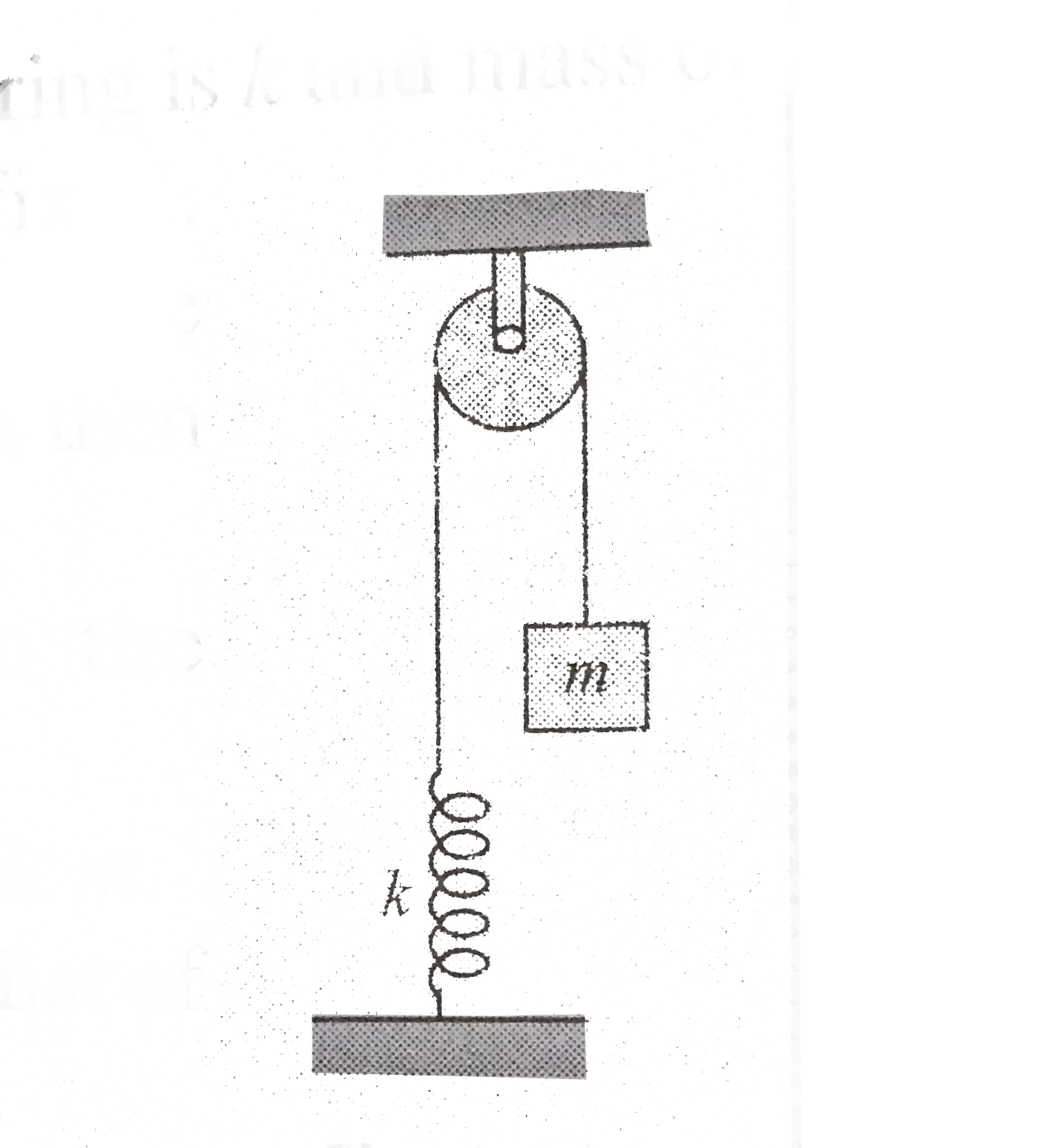
When the ball goes down by `x_0`, spring extends by `x_0`,
between (1) and (2)
Loss in gravitaion potential of ball `=` gain in energy of spring
`mgx_0=(1)/(2)kx_0^2impliesx_0(2mg)/(x_0)`
maximum extension of spring `=(2mg)/(x_0)`
Most of the students answer maximum extension `x_0=(mg)/(k_0)`
Which is wrong
When the ball is released, the spring extends. Let at some instant is `x`.

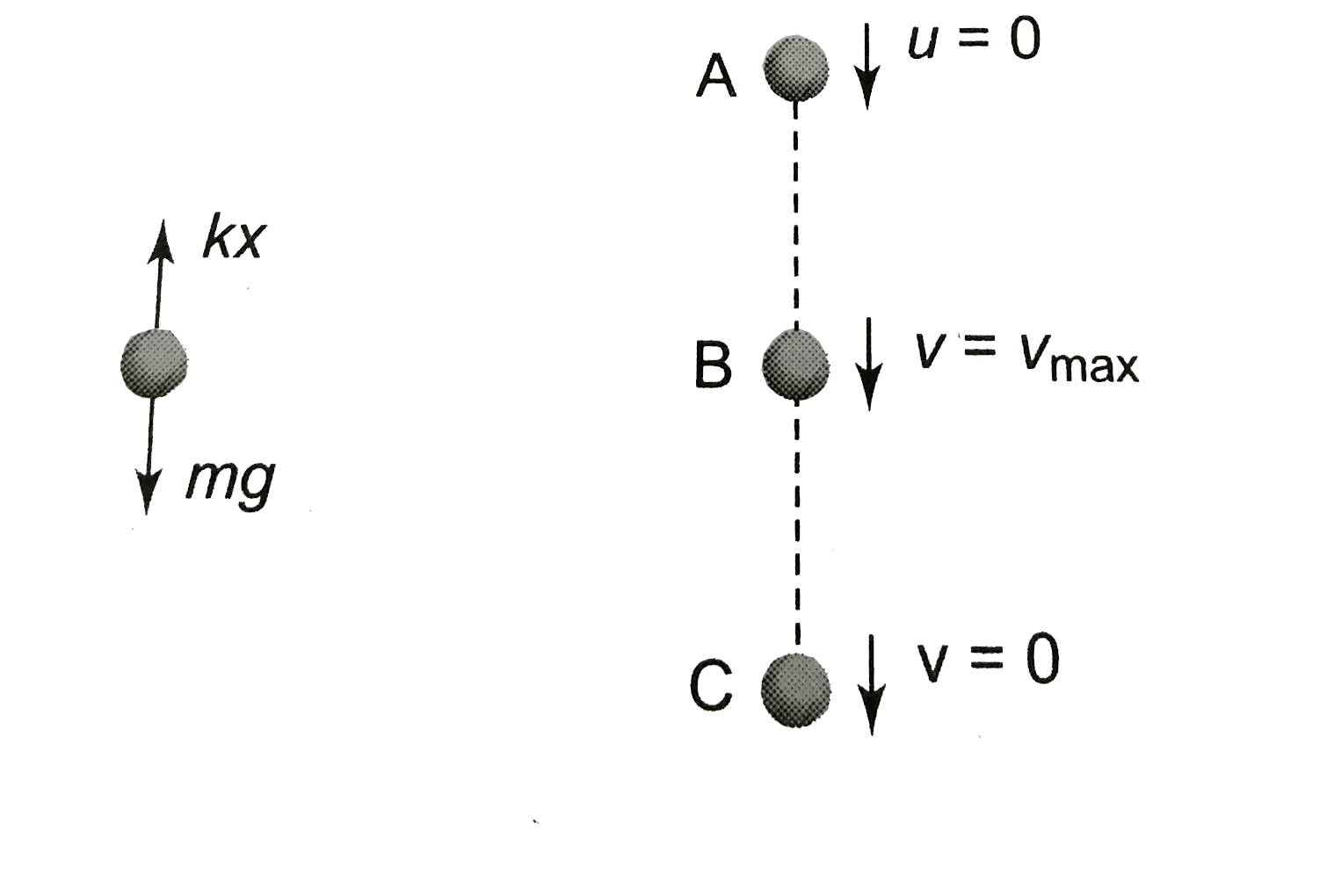
Now analyze the motion of ball:
A to B `mggtkx`, velocity of ball increases from 0 to `v_(max)` ltbRgt At B: `mg=kximpliesx=(mg)/(k)=x_0` the ball is in equilibrium,
velocity of the ball is maximum
B to C: `mgltkx`, velocity of the ball decreases to zero, the ball comes rest for a moment.
At C:

From C, the ball goes up and so on.