A uniform chain of length L and mass M overhangs a horizontal table with its two third part n the table. The friction coefficient between the table and the chain is μ. Find the work done by the friction during the period the chain slips off the table.
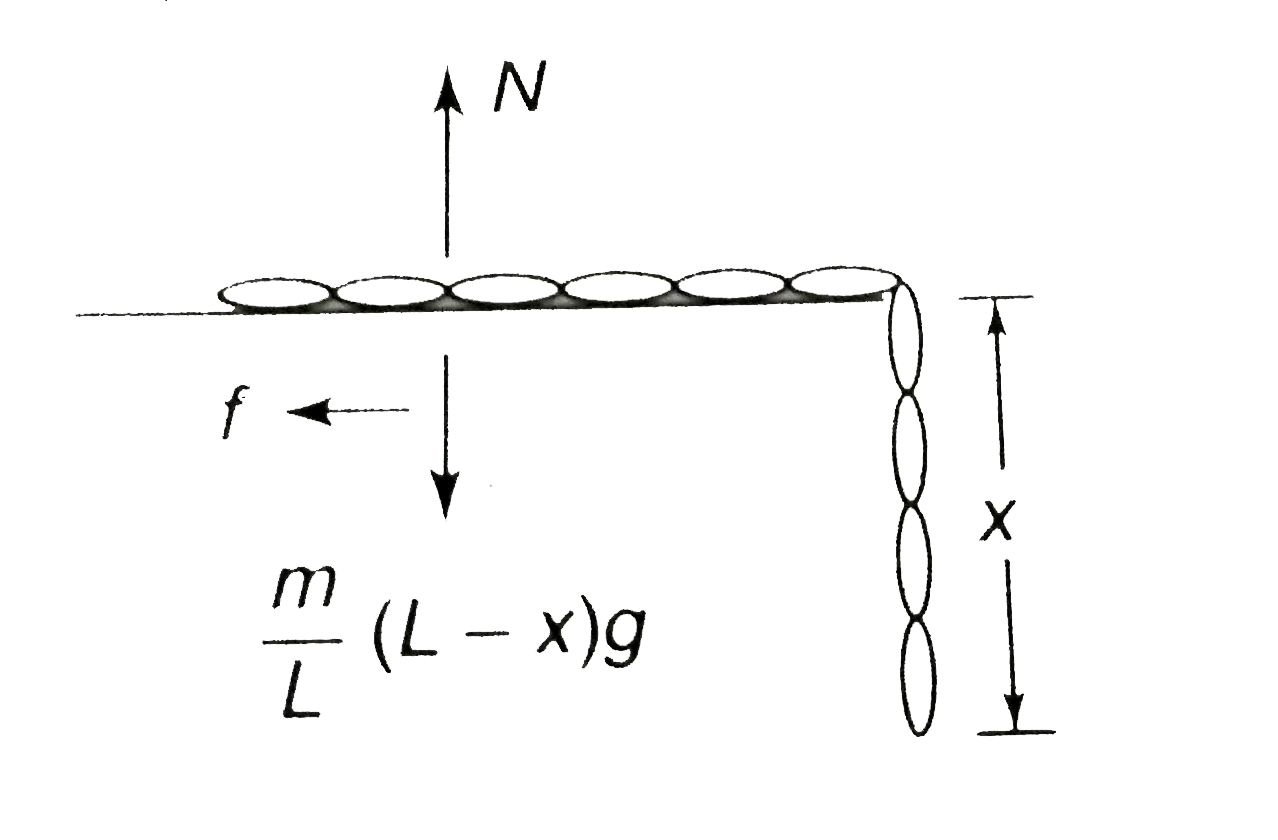
Let at some instant the hanging length is x. Friction acting on the chain
f=μmL(L−x)g
Small work done by friction during displacement dx
dW=−fdx
Total work done from x=L3 to x=L
W=−∫LL3μmgL(L−x)dx
=−μmgL∣∣∣Lx−x22∣∣∣LL3
=−μmgL[{L×L−L22}−{L×L3−12(L3)2}]
=−μmgL[(L22)−(5L218)]
=−μmgL.4L218=−2μmgL9
Topper's Solved these Questions
Similar Questions
AS uniform chain of length L and mass M overhangs a horizontal table with its two third part n the table. The friction coefficient between the tabe and the chian is μ. Find the work done by the friction during the period the chain slips off the table.
View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is µ. The work done by the friction during the period the chain slips off the table is [−2kμMgL]. Find the value of k.
View Solution
Knowledge Check
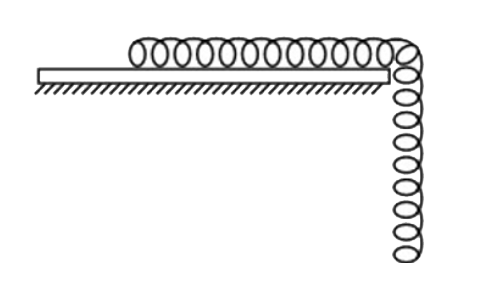
A uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then
 Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ)
Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ)A chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
 AμL1+μBμL1−μC(1−μ)L1+μDμL
AμL1+μBμL1−μC(1−μ)L1+μDμLA uniform chain of length L lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small portion of the chain is hanging over the edge. The chain starts sliding due to the weight of the hanging part
AThe acceleration of the chain is (gx/L), where x is the length of the hanging part of chain.BThe acceleration of the chain is (g/L)(L−x), where x is the length of hanging part of chain.CThe velocity of the chain is x√gL, where x is the length of hanging part of chain.DThe velocity of the chain is (L−x)√gL, where x is the length of hanging part of chain.
A uniform chain of length l and mass m overhangs a smooth table with its tow third pat lying on the tabl. Find the kinetic energy of the chain s it completely slips off the table.
View SolutionA uniform chain of mass m and length l overhangs a table with its two third part on the table. Fine the work to be done by a person to put the hanging part back on the table.
View SolutionA uniform chain of length L is lying partly on a table, the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5 what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground.
View SolutionA uniform chain of mass m and length l is at the verge of sliding under the effect of gravity of the hanging part. Find the

a. coefficient of friction, between chain and table.
b. work done by friction and gravity till the chain leaves the table if the hanging part is pulled gently and released.
c. speed of the chain at the time of leaving the table in part (b) .
d. work done by the external force acting at the end A of the chain in slowly pulling the chain completely onto the table.
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
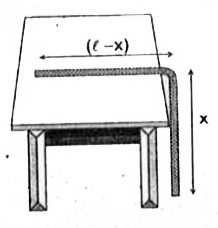
View Solution
