Two bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle α with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t.
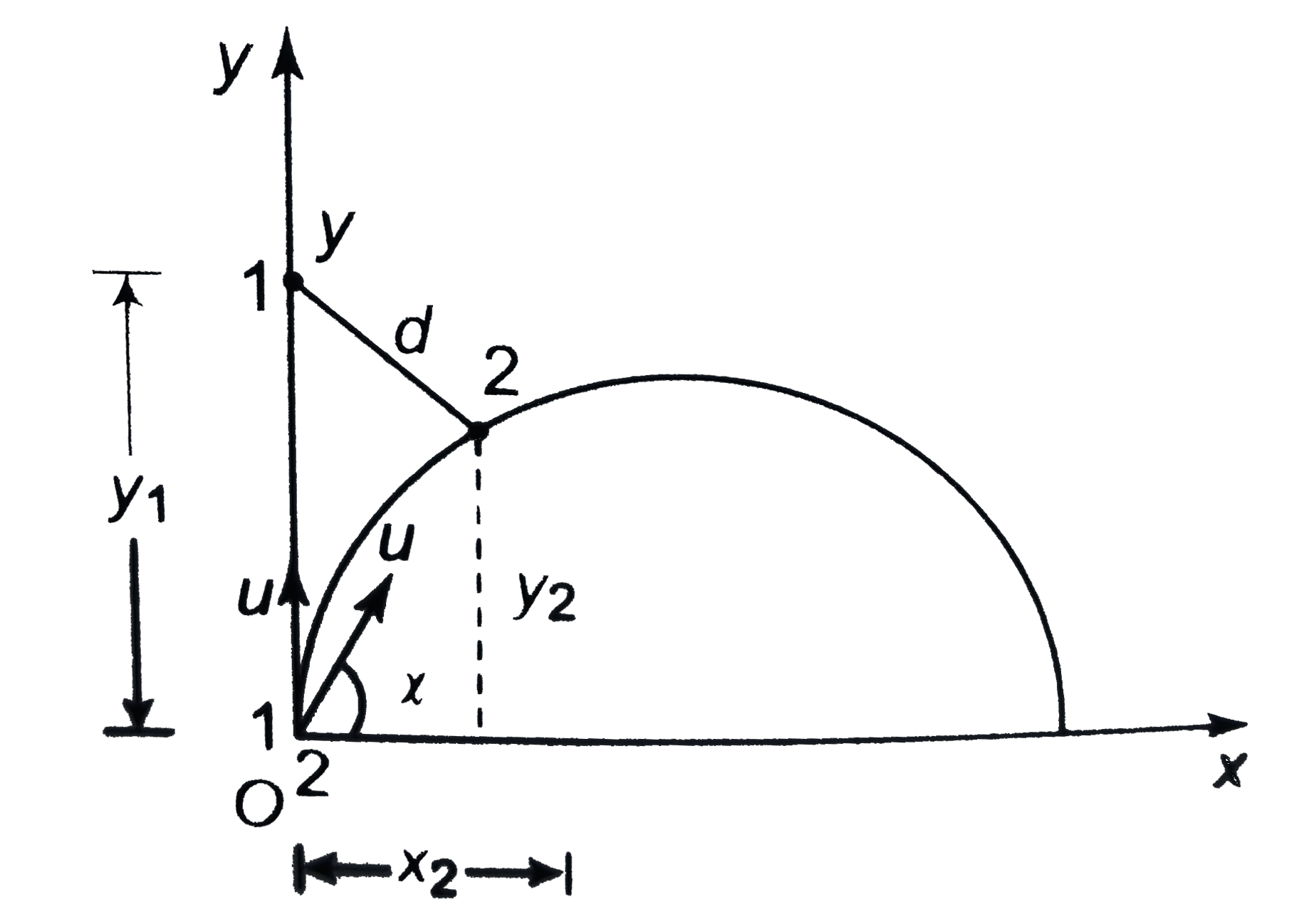
After time t
Particle 1: x1=0,y1=ut−12gt2
Particle 2: x2=ucosαt,y2=usinαt−12gt2
Distance between the particles
d=√(x2−x2)2+(y2−y1)2
=√(ucosαt−0)2+(usinαt−ut)2
=ut√cos2α+sin2α+1−2sinα
=ut√2−2sinα
=√2ut√1−sinα (i)
This answer can be expressed in other forms.
√1−sinα=√sin2(α)2+cos2(α)2−2sin(α)2cos(α)2
=cos(α)2−sin(α)2
d=√2ut(cos(α)2−sin(α)2) (ii)
cos(α)2−sin(α)2=√2(1√2cos(α)2−1√2sin(α)2)
=√2(cos(π)4cos(α)2−sin(π)4sin(α)2)
=√2cos(9π)4+α2)
d=√2ut√2cos(π4+α2)
=2utcos(π4+α2) (iii)
cos(π4+α2)=sin[π2−(π4+α2)]
=sin(π4+α2)
d=2utsin(π4−α2) (iv)
[cos(A+B)=cosAcosB−sinAsinBcos(A−B)=cosAcosB+sinAsinB]
Topper's Solved these Questions
Similar Questions
Two bodies were thrown simultaneously from the same point , on straight up and the other, at angle θ=60∘ to the horizontal . The initial velocity of each body is equal to u=30m/s. Neglecting the air resistance, find the distance between the bodies after 2 seconds.
View SolutionTwo bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of θ=60∘ to the horizontal. The initial velocity of each body is equal to v0=25m/s. Neglecting the air drag, find the distance between the bodies t=1.70s later.
View Solution
Knowledge Check
Two bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
A2v0t+12>2B2v0tCv0t+12g t2Dv0tTwo bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
A1 : 1Bsinθ:cosθCsin2θ:cos2θDcosθ:sinθTwo projectiles are thrown from the same point simultaneously with same velocity 10ms−1. One goes straight vertically while other at 60∘ with the vertical . What will be the distance of separation between the after 1 second of their throw?
A20mB10mC5mD15m
Two bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance (in meter) between the bodies at t=1.2 later is
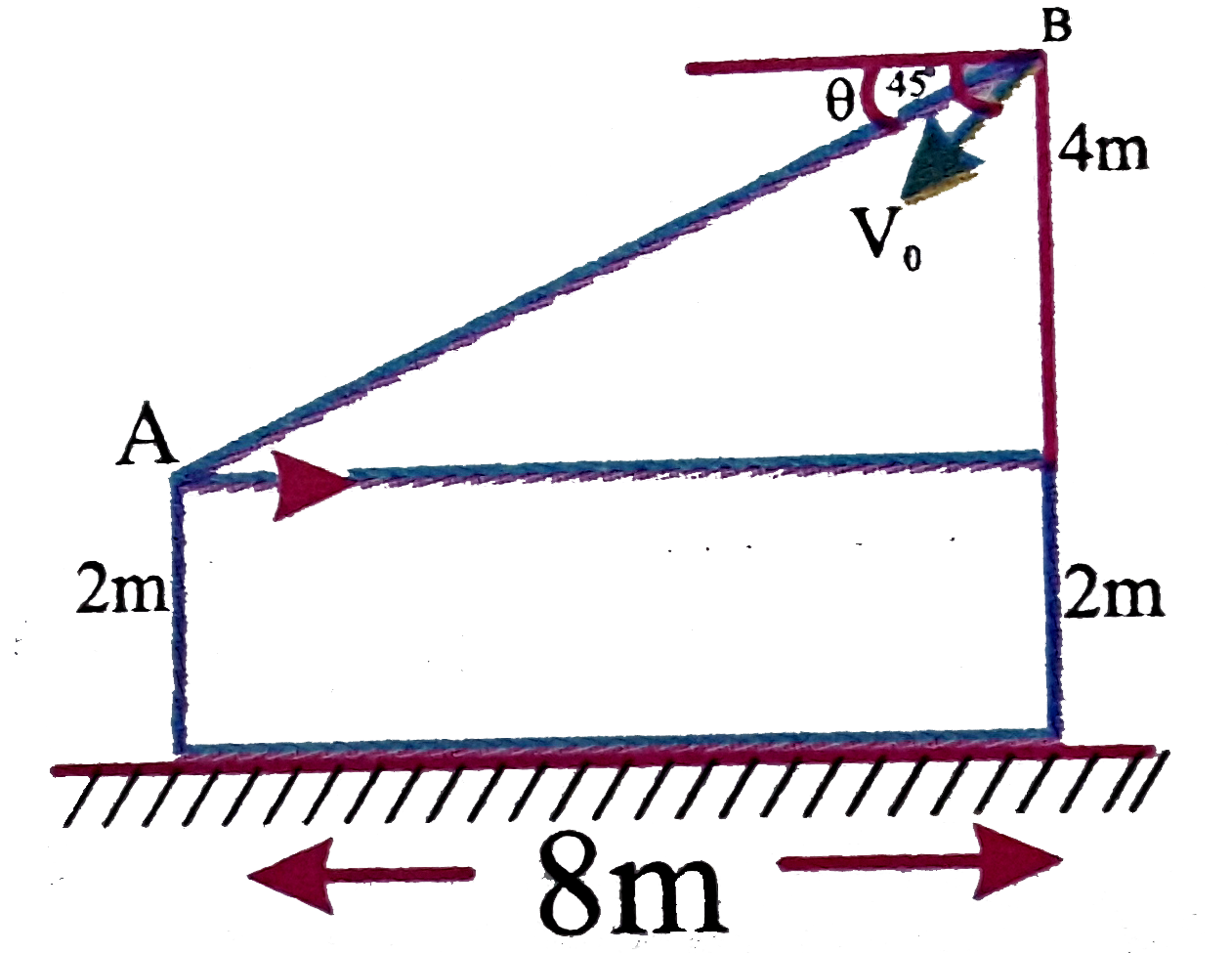
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneously towards each other, one is thrown horizontally with a velocity of 8m/s and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. This horizontal distance between points A and B equal to 8m.Then find
a)The initial velocity V0 of the body thrown at an angle 45∘
b)The time of flight t of the bodies before colliding
c) The coordinate (x,y) of the point of collision (consider the bottom of the tower A as origin )is
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of 8ms and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity V0 of the body thrown at an angle 45∘
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) is
View SolutionTwo bodies are thrown with the same velocity at angles α and 90∘−α to the horizontal.Calculate the ratio of the maximum heights reached by the bodies.
View SolutionA body of mass m is thrown upwards at an angle θ with the horizontal with velocity v. While rising up the velocity of the mass after t second will be
View Solution

