Question

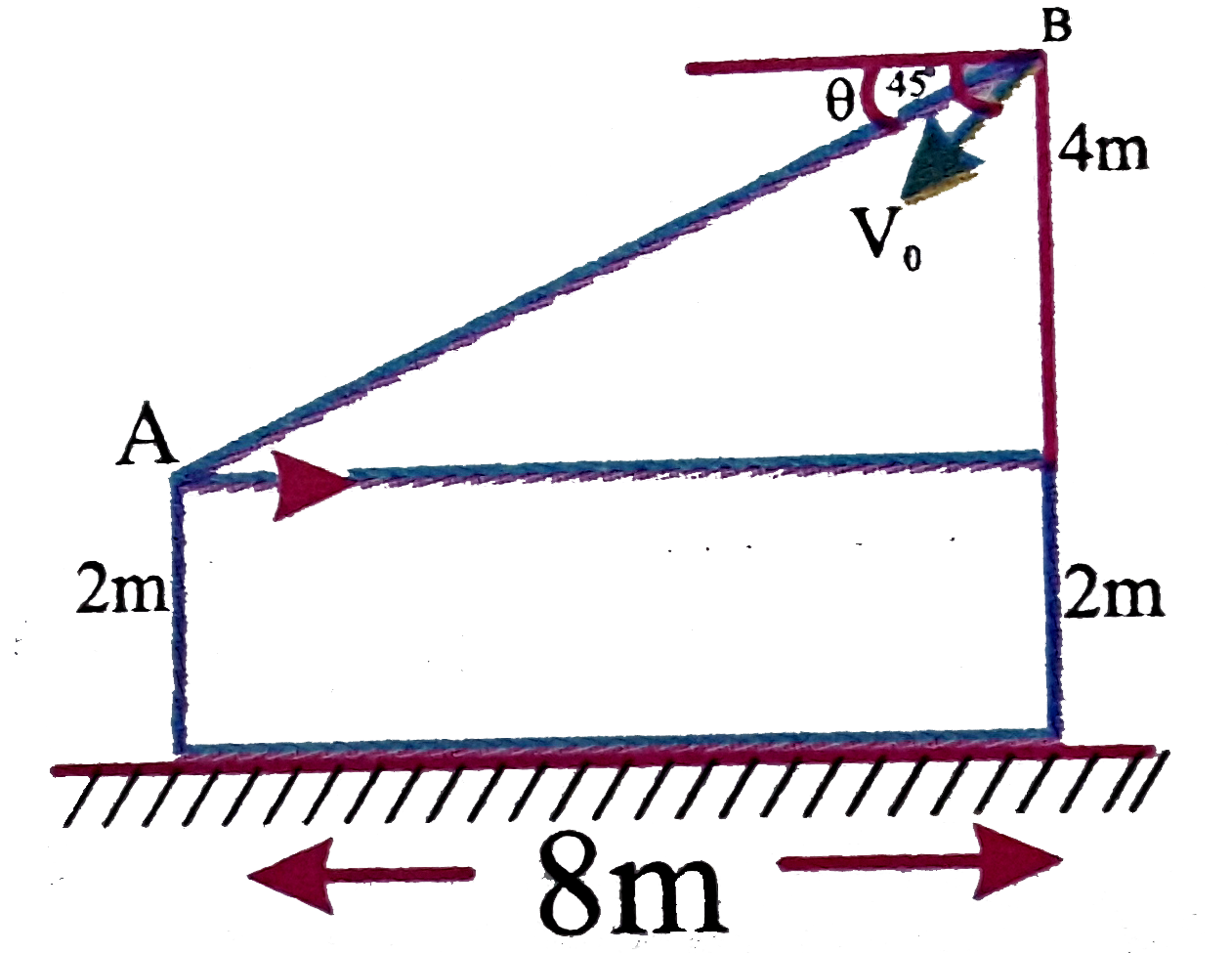
From points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of ${\displaystyle 8\frac{\text{m}}{s}}$ and the other, downward at an angle ${\displaystyle {45}^{\circ }}$ to the horizontal at an initial velocity ${\displaystyle v_0}$ such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity ${\displaystyle V_0}$ of the body thrown at an angle ${\displaystyle {45}^{\circ }}$
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) is

Explanation

To solve the problem step by step, we will follow the motion equations for both bodies and find the required values.

Step 1: Understand the Problem
We have two bodies thrown from points A and B. Body A is thrown horizontally from a height of 2 m with a velocity of 8 m/s, and body B is thrown downward at a 45-degree angle from a height of 6 m with an initial velocity \( V_0 \).

Step 2: Set Up the Coordinate System
We will set the bottom of tower A (height = 0) as the origin (0, 0). Therefore:
- The height of point A = 2 m (coordinates: (0, 2))
- The height of point B = 6 m (coordinates: (8, 6))

Step 3: Determine the Time of Flight
Let \( t \) be the time taken for the bodies to collide. The horizontal distance traveled by body A is given by:
\( x_A = 8 \cdot t \)

For body B, which is thrown at a 45-degree angle, the horizontal distance is:
\( x_B = V_0 \cdot \cos(45^\circ) \cdot t = \frac{V_0}{\sqrt{2}} \cdot t \)

Since the total horizontal distance between A and B is 8 m:
\( x_A + x_B = 8 \)
\( 8t + \frac{V_0}{\sqrt{2}} t = 8 \)
Factoring out \( t \):
\( t \left( 8 + \frac{V_0}{\sqrt{2}} \right) = 8 \)
Thus,
\( t = \frac{8}{8 + \frac{V_0}{\sqrt{2}}} \)

Step 4: Set Up the Vertical Motion Equations
For body A (thrown horizontally):
The vertical position \( y_A \) after time \( t \) is given by:
\( y_A = 2 - \frac{1}{2} g t^2 \)
Where \( g = 10 \, \text{m/s}^2 \).

For body B (thrown downward):
The vertical position \( y_B \) after time \( t \) is:
\( y_B = 6 - V_0 \cdot \sin(45^\circ) \cdot t - \frac{1}{2} g t^2 = 6 - \frac{V_0}{\sqrt{2}} t - \frac{1}{2} g t^2 \)

Step 5: Set Up the Height Difference Equation
The difference in heights when they collide is:
\( y_B - y_A = 4 \)
Substituting the equations for \( y_A \) and \( y_B \):
\( \left(6 - \frac{V_0}{\sqrt{2}} t - \frac{1}{2} g t^2\right) - \left(2 - \frac{1}{2} g t^2\right) = 4 \)
This simplifies to:
\( 6 - 2 - \frac{V_0}{\sqrt{2}} t = 4 \)
Thus:
\( 4 - \frac{V_0}{\sqrt{2}} t = 4 \)
This leads to:
\( -\frac{V_0}{\sqrt{2}} t = 0 \)

Step 6: Solve for \( V_0 \)
From the previous equation, we can isolate \( V_0 \):
\( V_0 = 8\sqrt{2} \)

Step 7: Calculate Time of Flight
Substituting \( V_0 \) back into the time equation:
\( t = \frac{8}{8 + \frac{8\sqrt{2}}{\sqrt{2}}} = \frac{8}{8 + 8} = \frac{8}{16} = 0.5 \, \text{s} \)

Step 8: Find the Coordinates of Collision
For body A:
\( x_A = 8 \cdot t = 8 \cdot 0.5 = 4 \, \text{m} \)

For the vertical position of body A at collision:
\( y_A = 2 - \frac{1}{2} \cdot 10 \cdot (0.5)^2 = 2 - \frac{1}{2} \cdot 10 \cdot 0.25 = 2 - 1.25 = 0.75 \, \text{m} \)

Thus, the coordinates of the collision point are:
\( (4, 0.75) \)

Summary of Results
- Initial velocity \( V_0 = 8\sqrt{2} \, \text{m/s} \)
- Time of flight \( t = 0.5 \, \text{s} \)
- Coordinates of collision \( (4, 0.75) \)