A radius vector of a point A relative to the origin varies with time t as r=ati−bt2j, where a and b are positive constants, and i and j are the unit vectors of the x and y axes. Find:
(a) the equation of the point's trajectory y(x), plot this function,
(b) the time dependence of the velocity v and acceleration w vectors, as well as of the moduli of these quantities,
(c) the time dependence of the angle α between the vectors w and v,
(d) the mean velocity vector averaged over the first t seconds of motion, and the modulus of this vector.
→r=αtˆi−βt2ˆj=xˆi+yˆj
(a) x=αt⇒t=xα
y=−βt2=−βx2α2
y=−βx2α2 (parabola, open downward)
(b) →r=αtˆi−βt2ˆj
→vd→rdt=αˆi−2β−2βtˆj
→a=d→vdt=02βˆj
|→v|=v=√(α)2+(−2β)2=√α2+4β2t2
|→a|=2β
( c) For the angle between →v and →a
→v.→a=4β2t
cosθ=→v.→a|→v||→a|=4β2t√α2+4β2t2(2β)
=2βt√α2+4β2t2
where θis the angle between →v and →a.
(d) →v=∫t0→vdt∫t0dt=∫t0(αˆi−2βtˆj)dtt
=αtˆi−2β.t22ˆjt
=αˆi−βtˆj
∣∣¯→v∣∣=√α2+β2t2
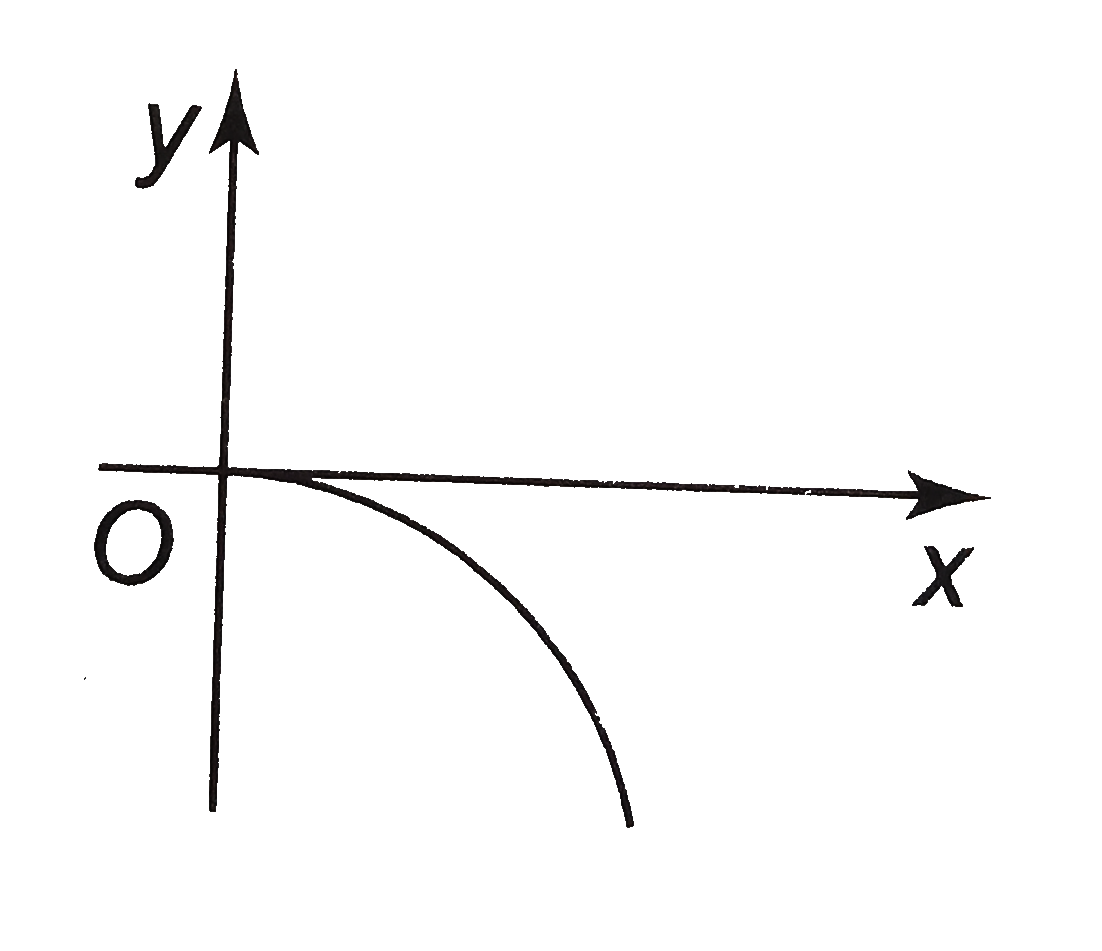
Topper's Solved these Questions
Similar Questions
A ardius vector of point A relative to the origin varies with time t as →r=atˆj−bt2ˆj where a and b are constants. Find the equation of point's trajectory.
View SolutionA point moves in the plane xy according to the law x=at, y=at(1−αt), where a and α are positive constants, and t is time. Find:
(a) the equation of the point's trajectory y(x), plot this function,
(b) the velocity v and the acceleration w of the point as functions of time,
(c) the moment t0 at which the velocity vector forms an angle π/4 with the acceleration vector.
View Solution
Knowledge Check
A radius vector of point A relative to the origin varies with time t as →r=atˆi−bt2ˆj where aandb are constant. The equation of point's trajectory is.
Ay=−ba2x2By=ba2x2Cy=−2ba2x2Dy=2ba2x2The velocity vector at a point A varies with time as →v=aˆi+btˆj , where a and b are positive constants. The equation of trajectory of the point would be
Ay=12bx2a2By=12ax2b2Cy=12axbDy=12bxaA force F=Ai+Bj is applied to a point whose radius vector relative to the origin of coordinates O is equal to r=ai+bj, where a, b, A, B are constants, and i,j are the unit vectors of the x and y axes. Find the moment N and the arm l of the force F relative to the point O.
AaB−Ab√A2+B2BaA−Bb√A2+B2CaB+Ab√A2+B2DAb−aB√A2+B2
Find the potential φ(x,y) of an electrostatic field E=2axyi+a(x4−y2)j, where a is a constant, I and J are the unit vectors of the x and y axes.
View SolutionA point moves in the x−y plane according to the equations x=at,y=at−vt2 Find : (a) the equation of the trajectory, (b) acceleration as s function of t (c) the instant t0 at which the velocity and acceleration are at π4.
View SolutionA point moves in the x-y plane according to the equations x=at, y=at-bt2.Find (a)the equation of the trajectory, (b)acceleration as a function of t, (c )the instant t0 at which the velocity and acceleration are at π/4 .
View SolutionA solid body rotates with angular velocity ω=ati+bt2j, where a=0.50rad/s2, b=0.060rad/s3, and i and j are the unit vectors of the x and y axes. Find:
(a) the moduli of the angular velocity and the angular acceleration at the moment t=10.0s,
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
View SolutionA particle moves in a plane such that its coordinates changes with time as x=at and y=bt, where a and b are constants. Find the position vector of the particle and its direction at any time t.
View Solution
