A solid body rotates with angular velocity ω=ati+bt2j, where a=0.50rad/s2, b=0.060rad/s3, and i and j are the unit vectors of the x and y axes. Find:
(a) the moduli of the angular velocity and the angular acceleration at the moment t=10.0s,
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
We have →ω=at→i+bt2→j (1)
So, ω=√(at)2+(bt2)2, thus, ω∣t=10s=7.81rad/s
Differentiating Eq. (1) with respect to time
→β=d→ωdt=a→i+2bt→j (2)
So, β=√a2+(2bt)2
and β∣t=10s=1⋅3rad/s2
(b) cosα=→ω⋅→βωβ=(at→i+bt2→j)⋅(a→i+2bt→j)√(at)2+(bt2)2√a2+(2bt)2
Putting the values of (a) and (b) and taking t=10s, we get
α=17∘
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
A solid body rotates with angular velocity →ω=3tˆi+2t2ˆjrad/s. Find
(a) the magnitude of angular velocity and angular acceleration at time t=1s and
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.
View SolutionA wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View Solution
Knowledge Check
A ball starts moving in a circular slot with angular acceleration α=2rad/s2 at t=0 The angle between its velocity and acceleration varies with time as
A90∘Btan−1(2t2)Ctan−1(t/2)D45∘The angular acceleration of a fan α=−3t22. At the initial moment, its angular velocity ω=10rad/s and has an angular position of 1 rad.
AIts angular velocity at t=1sec. Is 9.5 rad/sBits angular position at t=2 sec. Is 5 radCits angular velocity at t=2 sec. is 6 rad/sDits angualr position at t=1 sec. is 878 rad
The angular velocity and angular acceleration of the pivoted rod are given as ω and α respectively. Fid the x and y components of acceleration of B.
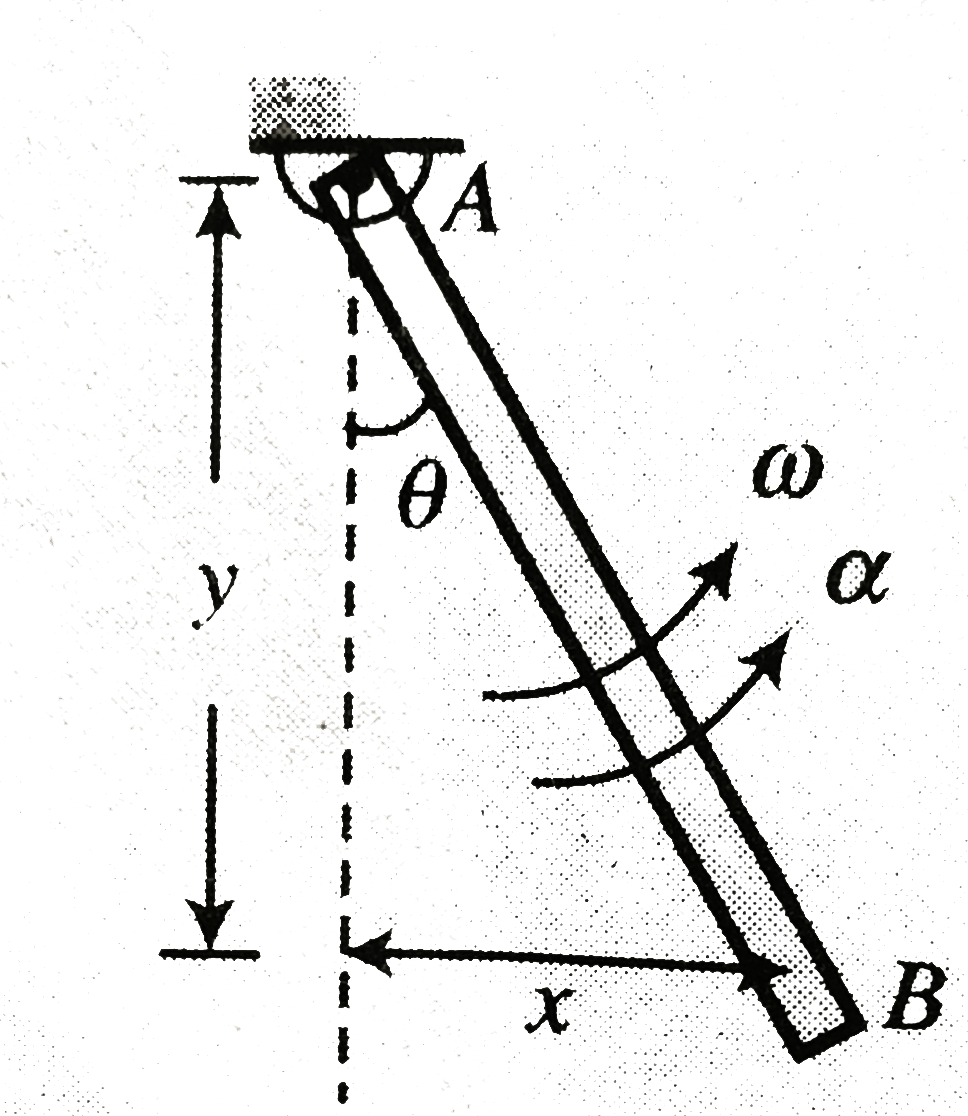
View SolutionA radius vector of a point A relative to the origin varies with time t as r=ati−bt2j, where a and b are positive constants, and I and j are the unit vectors of the x and y axes. Find:
(a) the equation of the point's trajectory y(x), plot this function,
(b) the time dependence of the velocity v and acceleration w vectors, as well as of the moduli of these quantities,
(c) the time dependence of the angle α between the vectors w and v,
(d) the mean velocity vector averaged over the first t seconds of motion, and the modulus of this vector.
View SolutionA particle is moving in a circle of radius 0.3 . Calculate its linear acceleration at the instant when its angular velocity is 1rad/s and angular acceleration is 4rad/s2
View SolutionWhat is the angular acceleration of a particle if the angular velocity of a particle becomes 4 times of its initial angular velocity 1 rad s in 2 seconds
View SolutionA wheel starting from rest via rotating with a constant angular velocity of 3 rad s−1. What is its angular acceleration after 4 s?
View SolutionA solid body rotates with a constant angular velocity ω0=0.50rad/s about a horizontal axis AB. At the moment t=0 the axis AB starts turning about the vertical with a constant angular acceleration β0=0.10rad/s2. Find the angular velocity and angular acceleration of the body after t=3.5s.
View Solution

