With what velocity (relative to the reference frame K) did the clock move, if during the time interval t=5.0s, measured by the clock of the frame K, it becomes slow by Δt=0.10s?
Because of time dilation, a moving clock reads less time. We write,
t−Δt=t√1−β2, β=vc
Thus, 1−2Δtt+(Δtt)2=1−β2
or, v=c√Δtt(2−Δtt)
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A rod moves lengthwise with a constant velocity v relative to the inertial reference frame K. At what value of v will the length of the rod in this frame be η=0.5% less than its proper length?
View SolutionThe reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to ˜E. Find the total energy E of this system of particles in the reference frame K.
View Solution
Knowledge Check
The velocity-time plot is shown in figure. Find the average speed in time interval t=0 to t=40s during the period.
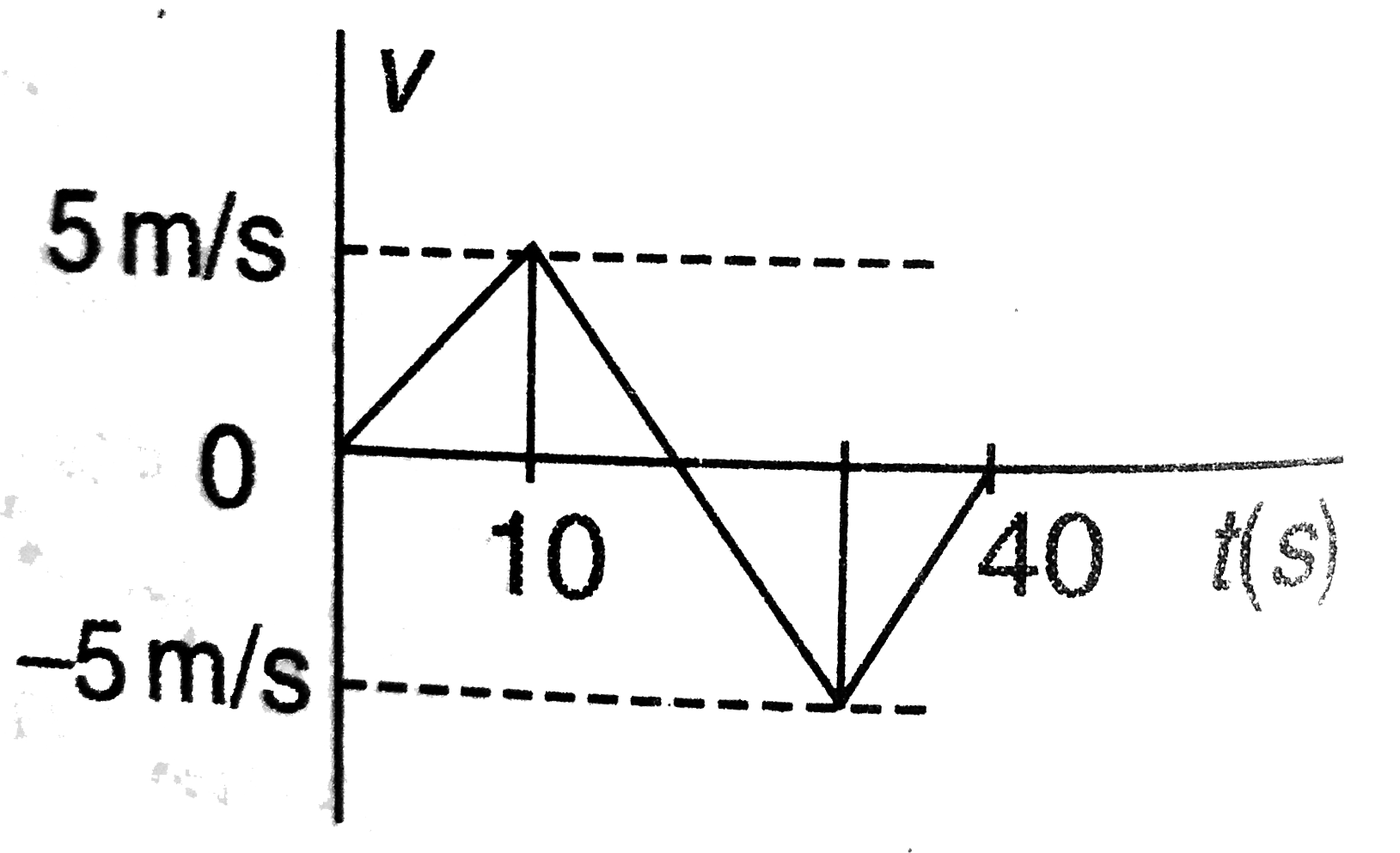 AzeroB2.5m/sC5m/sDnone
AzeroB2.5m/sC5m/sDnone
The frame K′ moves with a constant velocity V relative to the frame K. Find the acceleration w′ of a particle in the frame K′, if in the frame K this particle moves with a velocity v and acceleration w along a straight line
(a) in the direction of the vector V,
(b) perpendicular to the vector V.
View SolutionTwo rods of the same proper length l0 move toward each other parallel to a common horizontal axis. In the reference frame fixed to one of the rods the time interval between the moments, when the right and left ends of the rods coincide, is equal to Δt. What is the velocity of one rod relative to the other?
View SolutionA rod flies with constant velocity past a mark which is stationary in the reference frame K. In the frame K it takes Δt=20ns for the rod to fly past the mark. In the reference frame fixed to the rod the mark moves past the rod of Δt′=25ns. Find the proper length of rod.
View SolutionIn an inertial reference frame K there is only a unifrom electric field E=8kV/m in strength. Find the modulus and direction
(a) of the vector E' (b) of the vector B' in the interial refrernce frame K' moving with a constant velocity v relative to the frame K at an angle α=45∘ to the vector E. The velocity of the frame K' is equla to aβ=0.60 fraction of the velocity of light.
View SolutionA point A oscillates according to a certain harmonic law in the reference frame K′ which in its turn performs harmonic oscillations relative to the reference fromeK. Both oscillations occur along the same direction. When the K′ frame oscillates at the frequency 20 or 24Hz, the beat frequency of the point A in the K frame turns out to be equal to v. At what frequency of oscillation of the frame K′ will the beat frequency of the point A become equal to 2v?
View SolutionAn unstable particle moves in the reference frame K′ along its y′ axis with a velocity v′. In its turn, the frame K′ moves relative to the frame K in the positive direction of its x axis with a velocity V. The x′ and x axes of the two reference frames coincide, the y′ and y axes are parallel. Find the distance which the particle traverses in the frame K, if its proper lifetime is equal to Δt0.
View SolutionA plane electromagnetic wave propagates in a medium moving with constant velocity V<<c relative to an interial frame K. Find the velocity of that wave in the frame K if the refractive index of the medium is equal to n and the propagation direction of the wave coincides with that of the medium.
View Solution
