Two lead balls of masses m and 5m having radii R and 2R are separated by 12R. If they attract each other by gravitational force, the distance covered by small sphere before they touch each other is
10R
7.5R
9R
2.5R
The correct Answer is:B
To solve the problem, we need to find the distance covered by the smaller lead ball (mass m and radius R) before they touch each other. The larger lead ball has a mass of 5m and a radius of 2R, and they are initially separated by a distance of 12R.
1. Identify the Initial Setup:
- Mass of the smaller ball, m1=m
- Radius of the smaller ball, R1=R
- Mass of the larger ball, m2=5m
- Radius of the larger ball, R2=2R
- Initial separation between the centers of the balls, d=12R
2. Calculate the Distance Between the Centers When They Touch:
- When the two balls touch, the distance between their centers will be the sum of their radii:
dtouch=R1+R2=R+2R=3R
3. Determine the Final Distance Between the Centers:
- The initial distance between the centers is 12R. When they touch, the distance will be 3R.
- The distance that needs to be covered for them to touch is:
Δd=d−dtouch=12R−3R=9R
4. Calculate the Center of Mass:
- The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
- Let’s place the smaller ball at the origin (0, 0) and the larger ball at (12R, 0):
xCM=m⋅0+5m⋅12Rm+5m=60mR6m=10R
5. Determine the Distance Covered by the Smaller Ball:
- Let the distance covered by the smaller ball before they touch be x.
- The distance covered by the larger ball will be 9R−x since the total distance to be covered is 9R.
- The ratio of the distances covered by the two balls is inversely proportional to their masses:
x9R−x=5mm=5
- Cross-multiplying gives:
x=5(9R−x)
x=45R−5x
6x=45R
x=45R6=7.5R
Conclusion:
The distance covered by the smaller sphere before they touch each other is 7.5R.
- Mass of the smaller ball, m1=m
- Radius of the smaller ball, R1=R
- Mass of the larger ball, m2=5m
- Radius of the larger ball, R2=2R
- Initial separation between the centers of the balls, d=12R
- When the two balls touch, the distance between their centers will be the sum of their radii:
dtouch=R1+R2=R+2R=3R
- The initial distance between the centers is 12R. When they touch, the distance will be 3R.
- The distance that needs to be covered for them to touch is:
Δd=d−dtouch=12R−3R=9R
- The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
- Let’s place the smaller ball at the origin (0, 0) and the larger ball at (12R, 0):
xCM=m⋅0+5m⋅12Rm+5m=60mR6m=10R
- Let the distance covered by the smaller ball before they touch be x.
- The distance covered by the larger ball will be 9R−x since the total distance to be covered is 9R.
- The ratio of the distances covered by the two balls is inversely proportional to their masses:
x9R−x=5mm=5
- Cross-multiplying gives:
x=5(9R−x)
x=45R−5x
6x=45R
x=45R6=7.5R
The distance covered by the smaller sphere before they touch each other is 7.5R.
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL III
Explore 44 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:NCERT BASED QUESTIONS
Explore 26 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL I(C.W.)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
Two spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
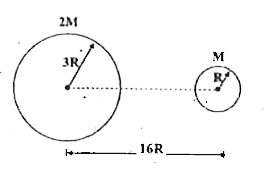
View Solution
Knowledge Check
Two spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
A15R2B13R2C10RD17R2Two spherical bodies of masses m and 4m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 15 R. If they attract each other due to gravitational force only, then the distance covered by smaller sphere just before collision will be
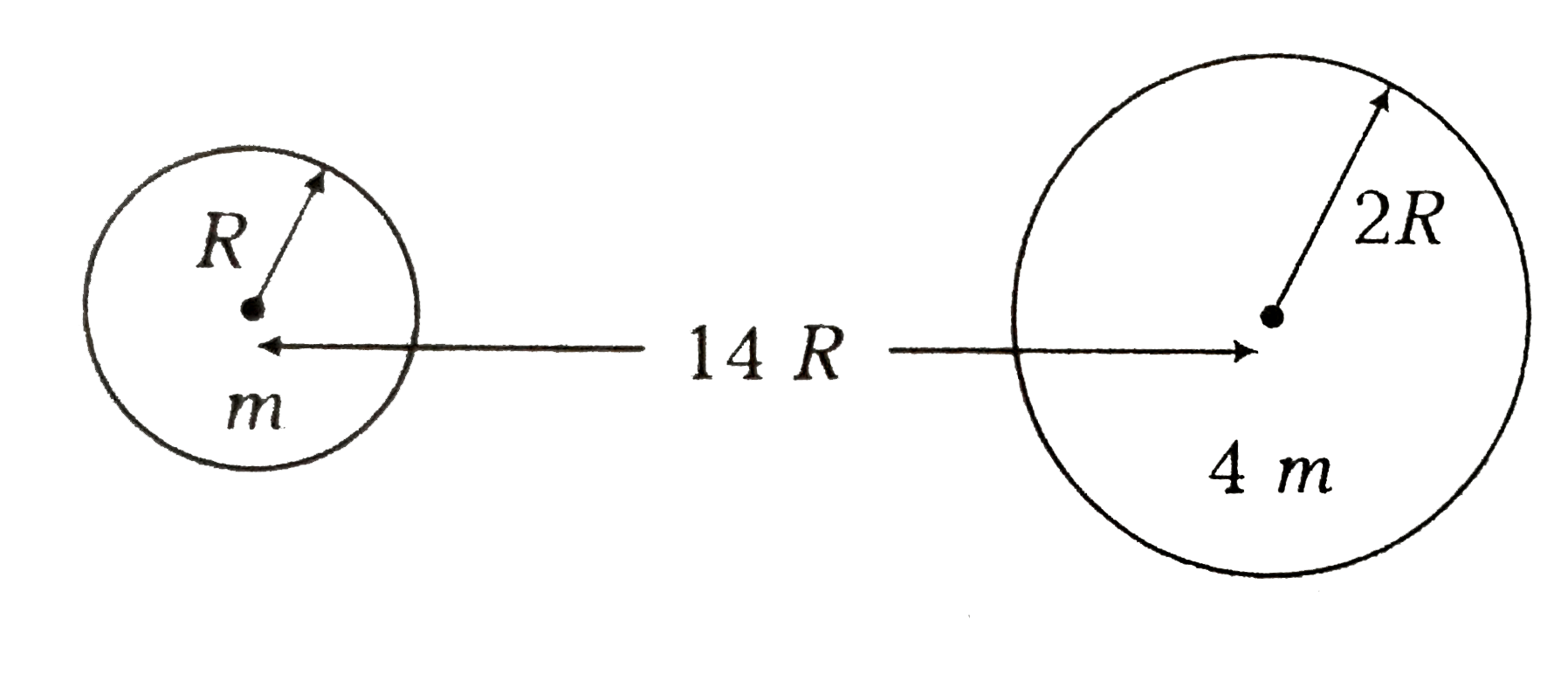 A5 RB9.6 RC2.5 RD6 R
A5 RB9.6 RC2.5 RD6 RTwo spherical bodies of masses m and 6m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 10 R . If they attract each other due to gravitational force only , then the distance covered by smaller sphere just before collisions will be
A6 RB7.5 RC2.5 RD9 R
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionWhich of the following statements is true ?
(i) A car of mass M is tied by one end of a massless rope of length 10m. The other end of the rope is in the hands of a man of mass M. The entire system is on a smooth horizontal surface.The man is at x=0 and the cart at x=10m. If the man pulls the cart by the rope, the man and the cart will meet at the point x=5m.
(ii) Two spherical bodies of mass M and 5M and radii R and 2R, respectively , are released in free space with initial separation between their centers equal to 12R. If they attract each other due to the gravitational force only , then the distance covered by the smaller body just before collision is 7.5R.
(iii) Two skaters A and B , having masses 40kg and 60kg , respectively stand facing each other 10m apart on a horizontal smooth surface. They pull on a rope stretched between them , the distance covered by A, when skaters meet is 6m.
(iv) A ballon (mass M) is attached to light rope of length L. To the other end of the rope a boy (mass m) is hanging in air. The system is at rest. The distance travelled by the balloon (in downward direction) when the boy touches the ballon is MLM+m.
View SolutionTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View SolutionTwo equal masses separated by a distance d attract each other with a force (F). If one unit of mass is transferred from one of them to the other, the force
View SolutionTwo identical spheres each of mass M and radius R are separated by a distance 3R. The force of attraction between them is proportional to
View Solution

