Two identical spheres each of mass M and radius R are separated by a distance 3R. The force of attraction between them is proportional to
The correct Answer is:B
To solve the problem, we will use Newton's law of universal gravitation, which states that the gravitational force F between two masses M1 and M2 separated by a distance r is given by the formula:
F=GM1M2r2
where G is the gravitational constant.
1. Identify the Masses and Distance:
- We have two identical spheres, each with mass M.
- The distance between the centers of the two spheres is given as 3R.
2. Apply the Gravitational Force Formula:
- According to the formula, the gravitational force F between the two spheres can be expressed as:
F=GM⋅M(3R)2
3. Simplify the Expression:
- Substitute the masses into the equation:
F=GM2(3R)2
- Calculate (3R)2:
(3R)2=9R2
- Therefore, the force becomes:
F=GM29R2
4. Determine the Proportionality:
- From the expression F=GM29R2, we can see that the force F is proportional to M2 and inversely proportional to R2.
- Thus, we can write:
F∝M2R2
Final Answer:
The force of attraction between the two spheres is proportional to M2R2.
- We have two identical spheres, each with mass M.
- The distance between the centers of the two spheres is given as 3R.
- According to the formula, the gravitational force F between the two spheres can be expressed as:
F=GM⋅M(3R)2
- Substitute the masses into the equation:
F=GM2(3R)2
- Calculate (3R)2:
(3R)2=9R2
- Therefore, the force becomes:
F=GM29R2
- From the expression F=GM29R2, we can see that the force F is proportional to M2 and inversely proportional to R2.
- Thus, we can write:
F∝M2R2
The force of attraction between the two spheres is proportional to M2R2.
Topper's Solved these Questions
- GRAVITATION Book:MARVEL PUBLICATIONChapter:GRAVITATION Exercise:TEST YOUR GRASP -2
Explore 20 Videos
- ELECTROSTATICSBook:MARVEL PUBLICATIONChapter:ELECTROSTATICSExercise:TEST YOUR GRASP
Explore 20 Videos
- INTERFERENCE AND DIFFRACTIONBook:MARVEL PUBLICATIONChapter:INTERFERENCE AND DIFFRACTIONExercise:TEST YOUR GRASP
Explore 20 Videos
Similar Questions
Knowledge Check
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GmrC−GM2rD−4GMrThe centres of a ring of mass m and a sphere of mass M of equal radius R, are at a distance √8R apart as shown. The force of attraction between the ring and the sphere is
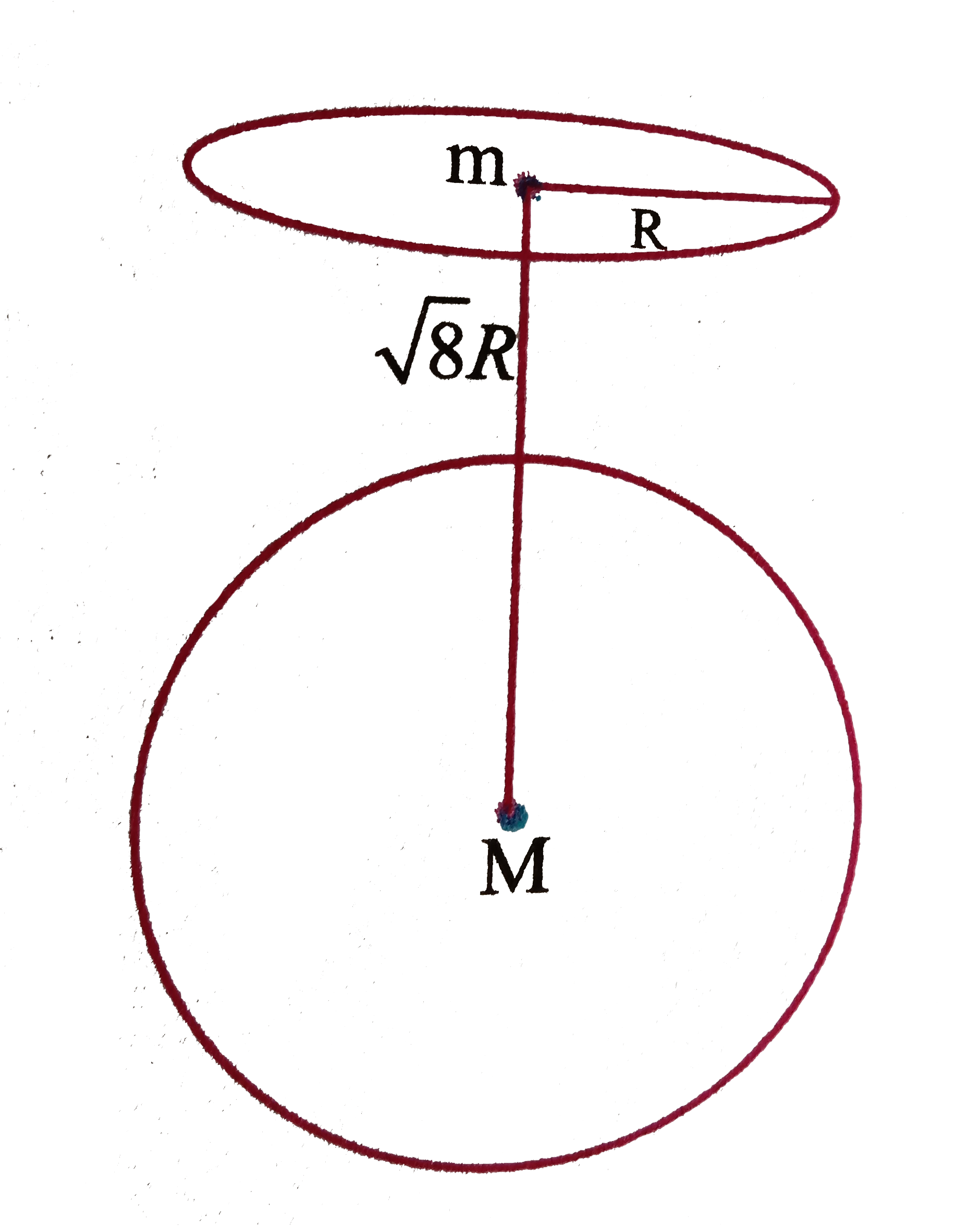 A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2
A2√227GmMR2BGmM8R2CGmM9R2D√29GmM9R2
Two balls, each of radius R, equal mass and density are placed in contact, then the force of gravitation between them is proportional to
View SolutionTwo identical spheres are placed in contact with each other. The force of gravitation between the spheres will be proportional to ( R = radius of each sphere)
View SolutionTwo identical spheres of radius R made of the same material are kept at a distance d apart. Then the gravitational attraction between them is proportional to
View SolutionForce of attraction between two point charges Q and −Q separated by dmetreisFe. When these charges are placed on two identical spheres of radius R=0.3d whose centres are dmetre apart , the force of attraction between them is
View SolutionTwo metallic spehres each of mass M and radius R charged separately to Q1 and Q2 are at a distance d between their centres (d>2R) The force between them will be
View Solution

