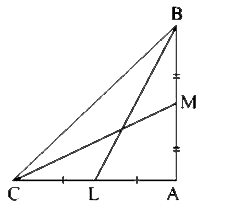
In △ABC,∠BAC=90∘ , seg BL and seg CM are medians of △ABC . Then prove that
4(BL2+CM2)=5BC2
The correct Answer is:∴4(BL2+CM2)=5BC2
Step by step video, text & image solution for In triangle ABC , angle BAC = 90^(@) , seg BL and seg CM are medians of triangle ABC . Then prove that 4 (BL^(2) + CM^(2)) = 5 BC^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Problem set-26
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Problem set-27
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Problem set-2
Explore 8 Videos
- PROBABILITYBook:TARGET PUBLICATIONChapter:PROBABILITYExercise:Try This
Explore 1 Video
- QUADRATIC EQUATIONSBook:TARGET PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:Additional problems for Practice : Based on Practice set 2.6
Explore 30 Videos
Similar Questions
Knowledge Check
In a ΔABC, angle BAC = 90∘. If BC = 25 cm, then what is the length of the median AD ?A24 cmB12.5 cmC14.5 cmD10 cm
BL and CM are medians of ΔABC, right - angled a A.
Prove that 4(BL2+CM2)=5 BC2
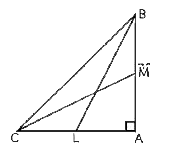
View Solutionseg AN and seg CM are the medians of △ABC in which ∠B=90∘ Prove that 4(AN2+CM2)=5AC2
View SolutionIn △ABC ,∠A=90∘. If BL and CM are medians, then:
△ABC में, ∠A=90∘ है | यदि BL और CM मध्थिकाएं हैं, तो :
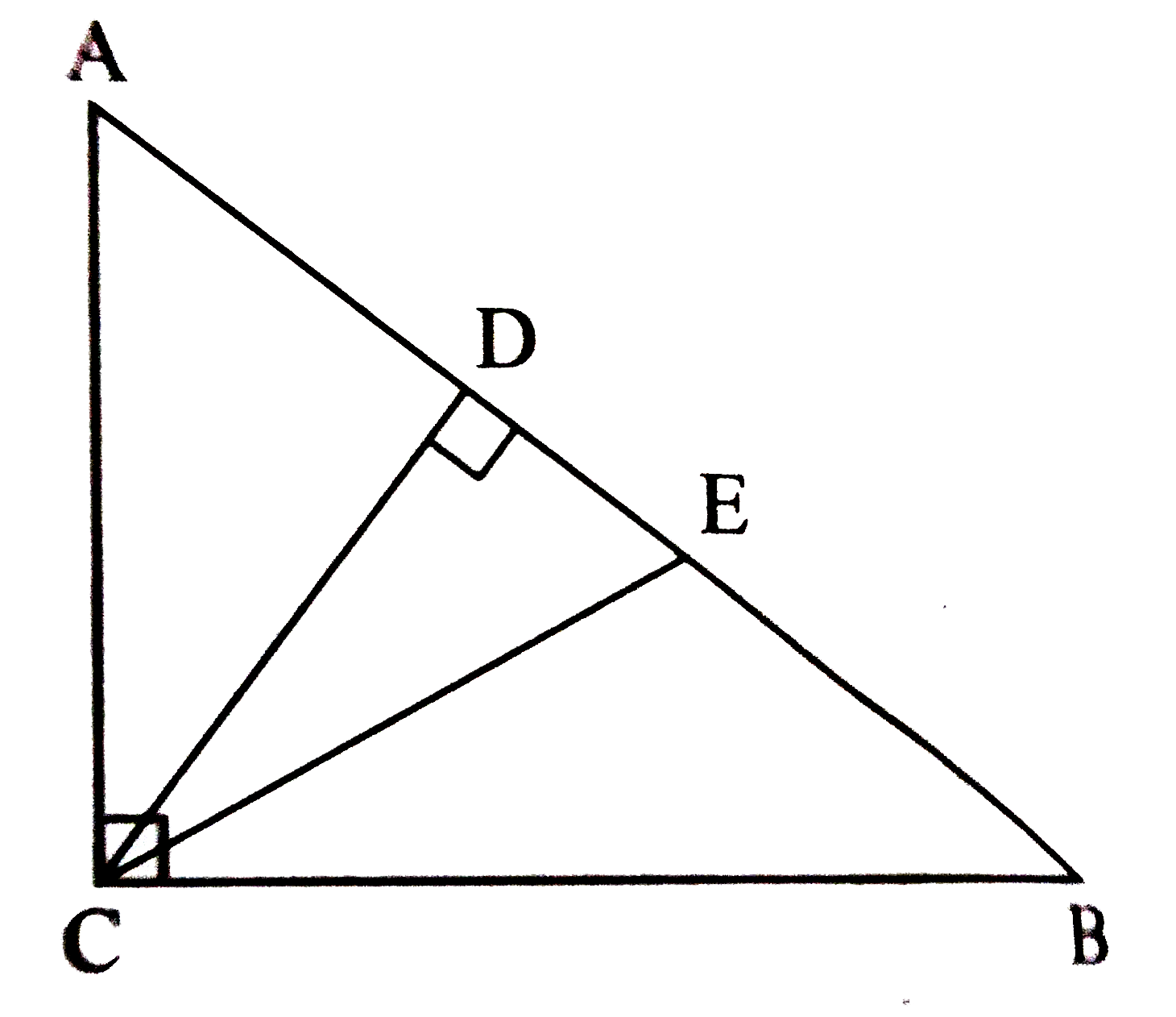
View SolutionIn ΔABC,∠ACB=90∘, seg CD⊥ side AB and seg CE is angle bisector of ∠ACB
Prove : ADBD=AE2BE2
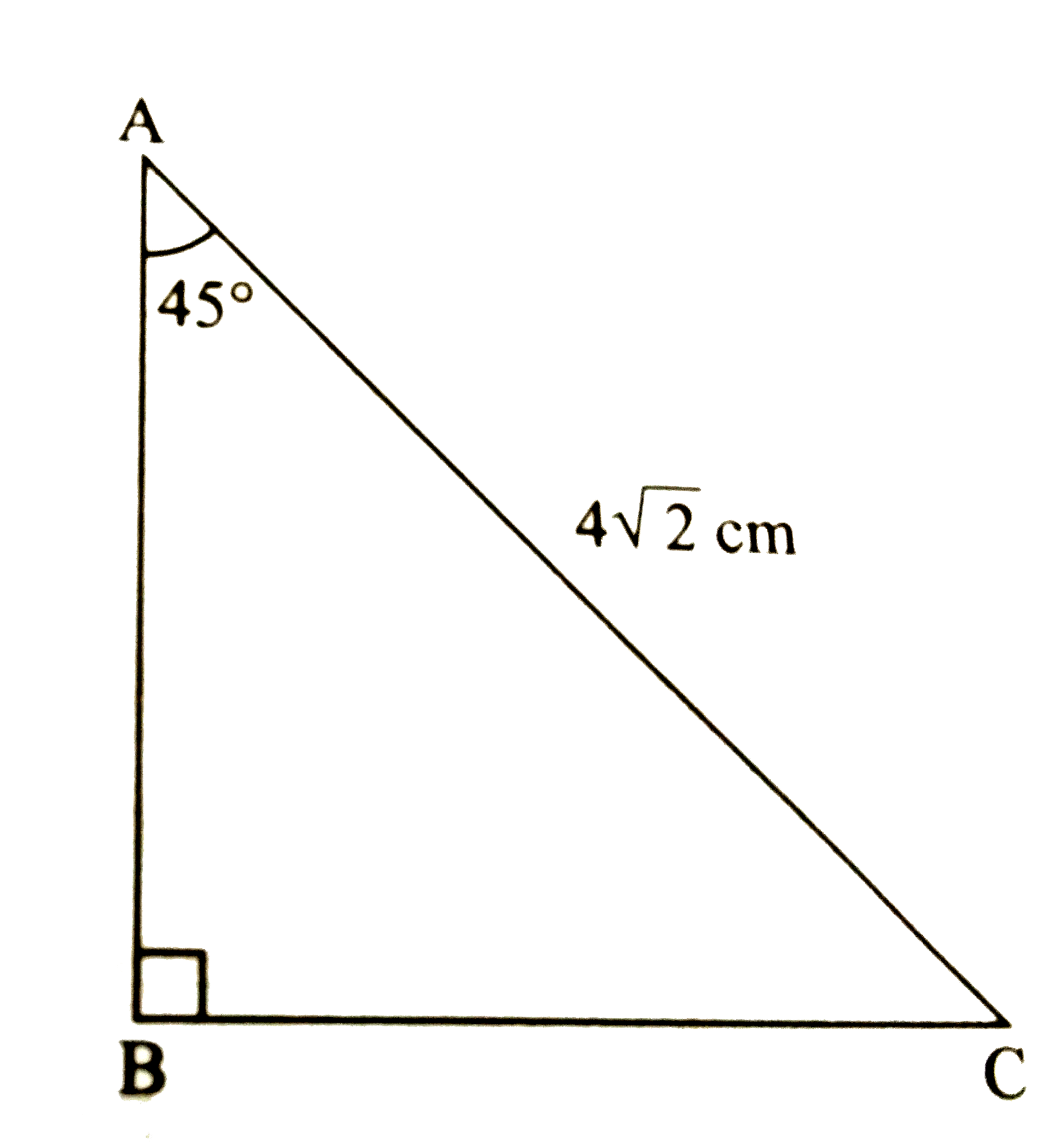
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
View SolutionIn a △ABC,∠A=90∘, if BM and CN are two medians, BM2+CN2BC2 is equal to:
△ABC में, ∠A=90∘, अगर BM और CN दो मध्यिका हैं, तो BM2+CN2BC2 बराबर है:
View Solution