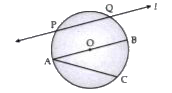
Consider a circles S with centre at the origin and radius 4. Four circles A, B, C and Deach with radiusunity and centres $(- 3, 0), (- 1, 0), (1, 0)$ and $(3, 0)$ respectively are drawn. A chord PQ of the circle Sne circle B and passes through the centre of the circle C. If the length of this chord can beexpressed as $\sqrt{x}$ , find x.

Video Solution

Answer

Step by step video, text & image solution for Consider a circles S with centre at the origin and radius 4. Four circles A, B, C and Deach with radiusunity and centres (-3, 0), (-1,0), (1,0) and (3, 0) respectively are drawn. A chord PQ of the circle Sne circle B and passes through the centre of the circle C. If the length of this chord can beexpressed as sqrtx , find x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Knowledge Check

A chord that passes through the centre of a circle is___
ADiameter
BSegment
CRadius
DCentre
The chord of a circle which passes through the centre is___the radius
AThrice
BDouble
CHalf
DEqual to
Equation of the circle with centre at (1,-2) , and passing through the centre of the circle $x^{2} + y^{2} + 2 y - 3 = 0$ , is
A $x^{2} + y^{2} - 2 x + 4 y + 3 = 0$
B $x^{2} + y^{2} - 2 x + 4 y - 3 = 0$
C $x^{2} + y^{2} + 2 x - 4 y - 3 = 0$
D $x^{2} + y^{2} + 2 x - 4 y + 3 = 0$

ARIHANT MATHS-CIRCLE -Exercise (Single Integer Answer Type Questions)

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

A chord that passes through the centre of a circle is___

The chord of a circle which passes through the centre is___the radius

Equation of the circle with centre at (1,-2) , and passing through the centre of the circle x2+y2+2y−3=0 , is

ARIHANT MATHS-CIRCLE -Exercise (Single Integer Answer Type Questions)

Equation of the circle with centre at (1,-2) , and passing through the centre of the circle $x^{2} + y^{2} + 2 y - 3 = 0$ , is