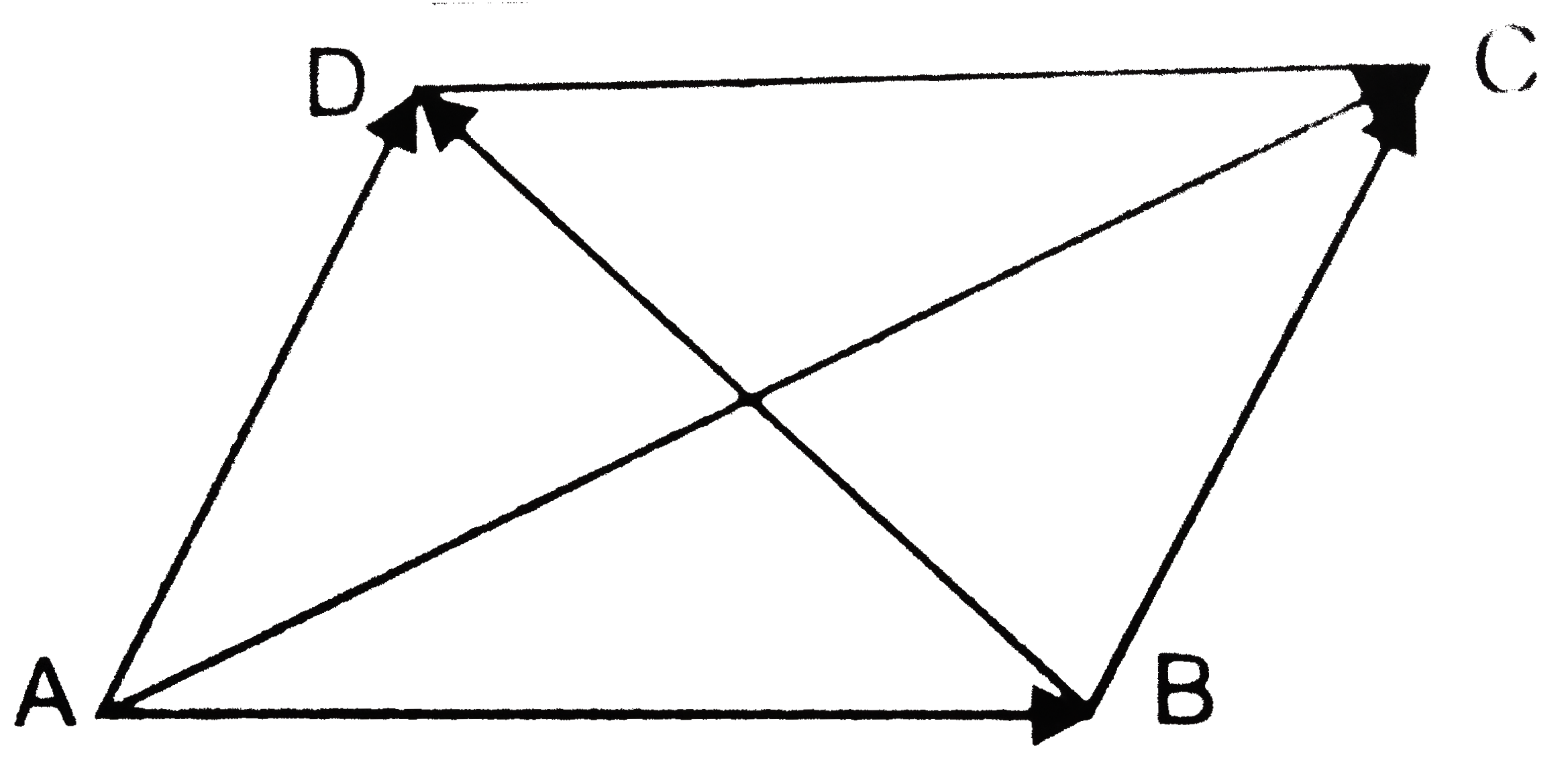
Let ABCD is a parallelogram and →AC,→BD be its diagonal, then →AC+→BD is
2¯¯¯¯¯¯AB
2¯¯¯¯¯¯BC
¯¯¯¯¯¯AB
¯¯¯¯¯¯BC
The correct Answer is:B
Step by step video, text & image solution for Let ABCD is a parallelogram and vecAC, vecBD be its diagonal, then vecAC +vec BD is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a parallelogram, then −−→AC−−−→BD=
A4−−→ABB3−−→ABC2−−→ABD−−→AB - Question 2 - Select One
ABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
A4A→BB3A→BC2A→BDA→B - Question 3 - Select One
ABCD is a parallelogram and BD is a diagonal. ∠BAD=65∘ and ∠DBC=45∘, then m ∠BDC is :
A65∘B70∘C20∘Dnone of these
If →aand→b represent two adjacent sides →ABand→BC respectively of a parallelogram ABCD, then show that its diagonals →ACand→DB are equal to →a+→b and →a−→b respectively.
View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
. View SolutionABCD is a parallelogram where AC and BD are the diagonals. If ∠BAD=60∘,∠ABD=90∘, then what is BD2 equal to ?
View SolutionIf G is the intersection of diagonals of a parallelogram ABCD and O is any point, then O→A+O→B+O→C+−−→OD=
View SolutionIf G is the intersection of diagonals of a parallelogram ABCD and O is any point, then O→A+O→B+O→C+−−→OD=
View Solution