If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =
¯¯¯¯¯¯AC
¯¯¯O
¯¯¯¯¯¯CA
2¯¯¯¯¯¯CA
The correct Answer is:D
Step by step video, text & image solution for If ABCD is a square, then bar(AB) + 2 bar(BC) + 3 bar(CD) + 4 bar(DA) = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABCD is a square then,
2¯¯¯¯¯¯AB+4¯¯¯¯¯¯BC+5¯¯¯¯¯¯CD+7¯¯¯¯¯¯DA=A2¯¯¯¯¯¯BDB3¯¯¯¯¯¯CAC5¯¯¯¯¯¯DBD2¯¯¯¯¯¯ACIf ABCDE is a pentagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AE+¯¯¯¯¯¯BC+¯¯¯¯¯¯DC+¯¯¯¯¯¯ED=
A¯¯¯¯¯¯ACB2¯¯¯¯¯¯ACC2¯¯¯¯¯¯ADD3¯¯¯¯¯¯ADIf ABCDE is a regular penatagon then :
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AD+¯¯¯¯¯¯ED+¯¯¯¯¯¯AE=A¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCB3¯¯¯¯¯¯AC−2¯¯¯¯¯¯DCC¯¯¯¯¯¯CA−¯¯¯¯¯¯DCD3¯¯¯¯¯¯AC−¯¯¯¯¯¯DC
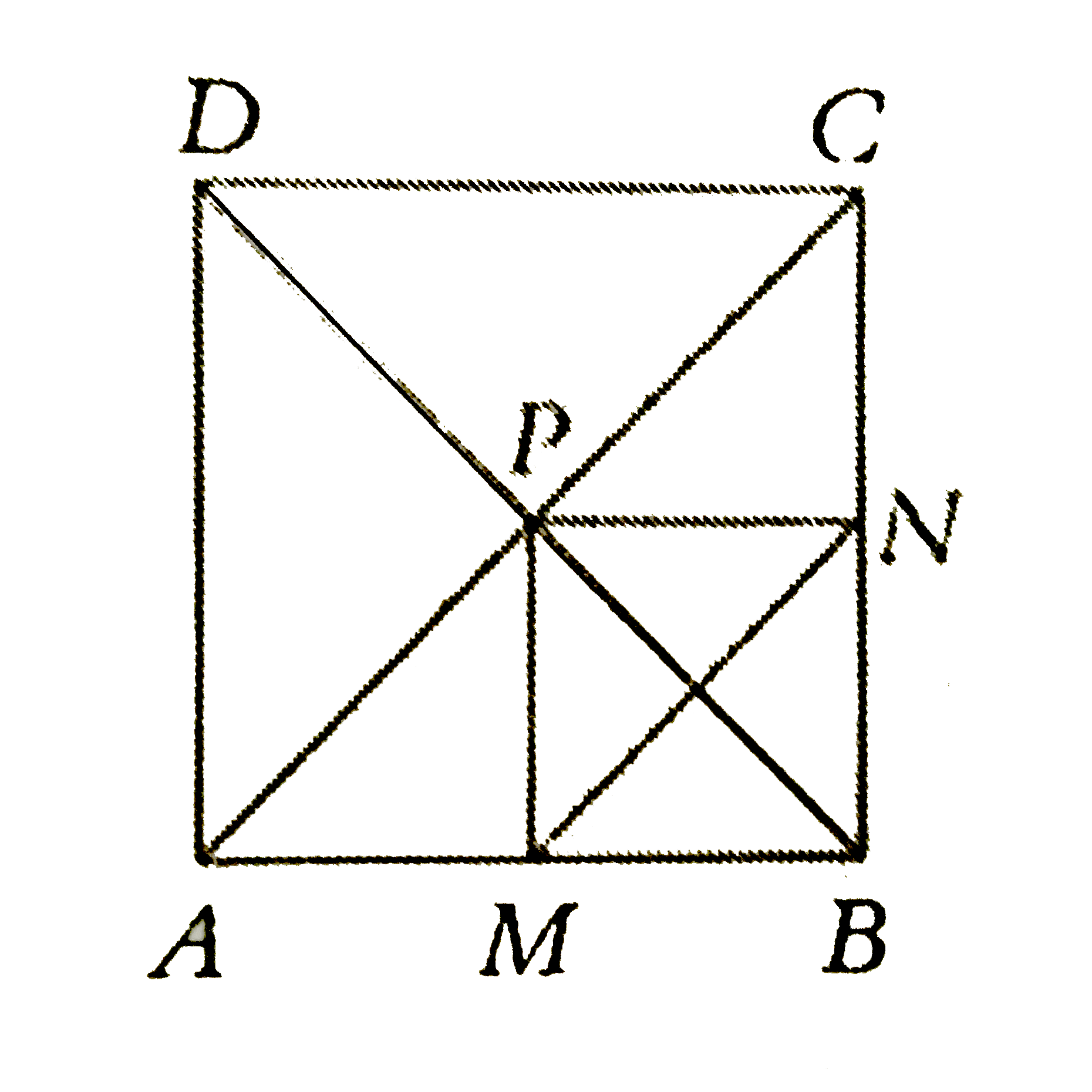
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.
View Solution
In the figure above, ABCD is a square of side 18 cm and ¯¯¯¯¯¯PN⊥¯¯¯¯¯¯BCand¯¯¯¯¯¯¯PM⊥¯¯¯¯¯¯AB. Find the length of MN.
View Solution
In the figure above, ABCD is a parallelogram, ¯¯¯¯¯¯BE⊥¯¯¯¯¯¯AB,¯¯¯¯¯¯BG⊥¯¯¯¯¯¯CD, and EBGD is a square. If BG=12 cm and BC=13 cm , then find AB.
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View SolutionΔABC is an isosceles triangle and ¯¯¯¯¯¯AB=¯¯¯¯¯¯AC=2aunit, ¯¯¯¯¯¯BC = a unit. Draw AD⊥BC, and find the length of ¯¯¯¯¯¯AD .
View Solution
