OABC is a tetrahedron D and E are the mid points of the edges −−→OA and −−→BC. Then the vector −−→DE in terms of −−→OA,−−→OBand−−→OC
¯¯¯¯¯¯OC⊥¯¯¯¯¯¯AB
¯¯¯¯¯¯OC=¯¯¯¯¯¯AB
¯¯¯¯¯¯OC=2¯¯¯¯¯¯AB
¯¯¯¯¯¯OC=¯¯¯¯¯¯AB
The correct Answer is:A
Step by step video, text & image solution for OABC is a tetrahedron D and E are the mid points of the edges vec (OA) and vec (BC). Then the vector vec(DE) in terms of vec(OA), vec (OB) and vec(OC) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
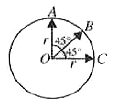 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1)If OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :A[ˆaˆbˆc][ˆpˆqˆr]=3√32B[ˆa+ˆb ˆb+ˆc ˆc+ˆa][ˆp+ˆq ˆq+ˆr ˆr+ˆp]=3√34C[ˆa+ˆb ˆb+ˆc ˆc+ˆa][ˆpˆqˆr]=3√32D[ˆaˆbˆc][ˆp+ˆq ˆq+ˆr ˆr+ˆp]=3√34If OAB is a tetrahedron with edges and ˆp,ˆq,ˆr are unit vectors along bisectors of
−−→OA,−−→OB:−−→OB,−−→OC:−−→OC,−−→OA respectively and ˆa=−−→OA∣∣∣−−→OA∣∣∣,→b=−−→OB∣∣∣−−→OB∣∣∣,→c=−−→OC∣∣∣−−→OC∣∣∣, then :A[ˆaˆbˆc][ˆpˆqˆr]=3√32B[ˆa+ˆb ˆb+ˆc ˆc+ˆa][ˆp+ˆq ˆq+ˆr ˆr+ˆp]=3√34C[ˆa+ˆb ˆb+ˆc ˆc+ˆa][ˆpˆqˆr]=3√32D[ˆaˆbˆc][ˆp+ˆq ˆq+ˆr ˆr+ˆp]=3√34
The resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
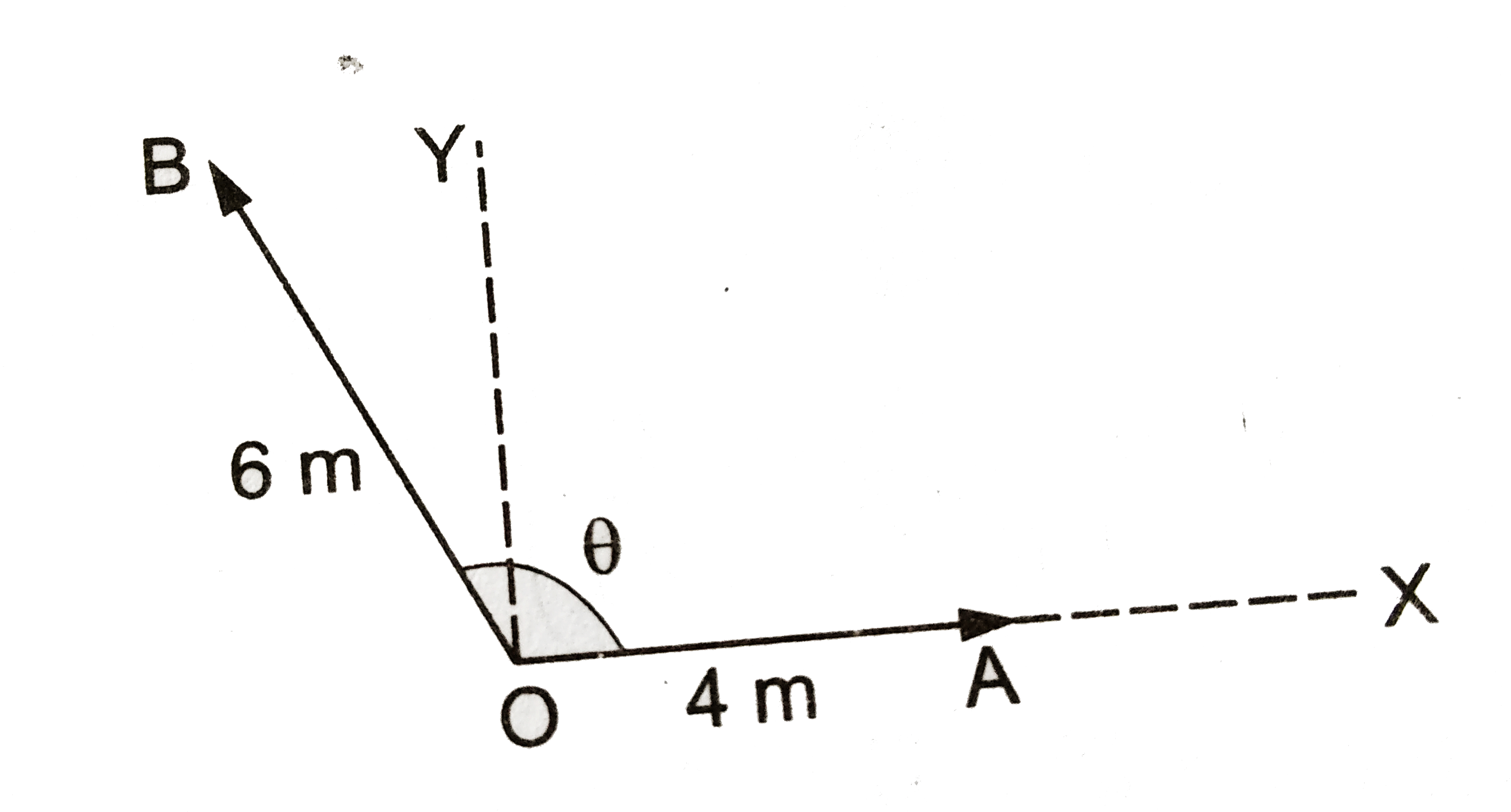
View SolutionRefer to figure Find a the magnitude, b x and y components and c. the angle with the X-axis of the resultant of −−→OA,−−→BCand−−→DE.
 .
.
View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View SolutionABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of −−→OA , −−→OB , −−→OC and −−→OD = 4 −−→OE , where O is any point.
View Solution

 .
.