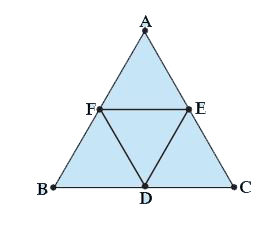
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
(i) ΔABC में
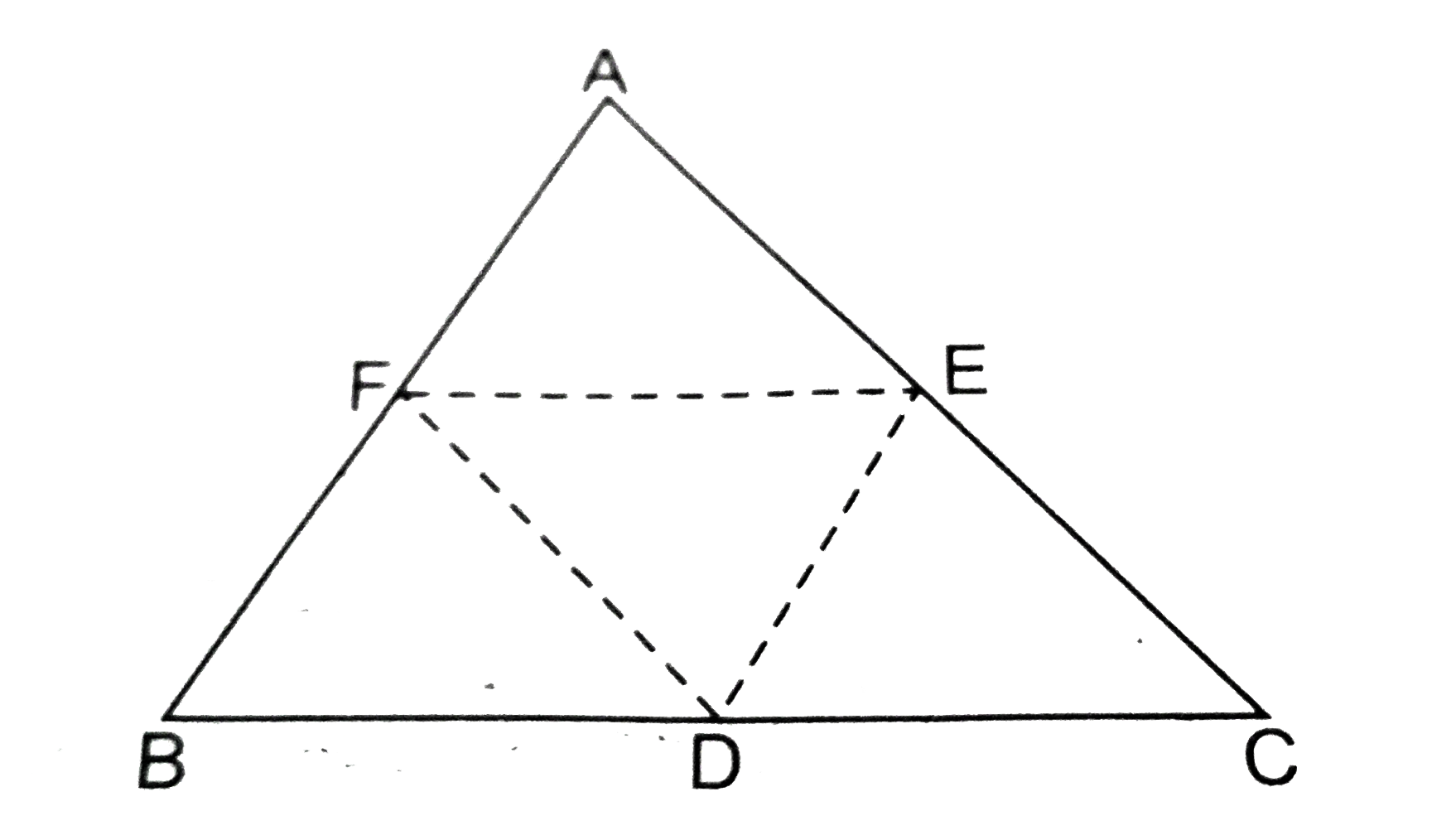
AB का मध्य-बिन्दु F और AC का मध्य-बिन्दु E है।
∴ FE || BC
⇒ FE || BD
इसी प्रकार ED || FB
∴□BDEF एक समान्तर चतुर्भुज है।
(ii) □BDEF एक समान्तर चतुर्भुज है तथा FD इसका विकर्ण है।
∴ΔFBD का क्षेत्रफल =ΔDEF का क्षेत्रफल ...(1)
इसी प्रकार सिद्ध कर सकते है कि
ΔCDE का क्षेत्रफल =ΔDEF का क्षेत्रफल ...(2)
और ΔAFE का क्षेत्रफल =ΔDEF का क्षेत्रफल ...(3)
∴4×ΔDEF का क्षेत्रफल
=ΔDEF का क्षेत्रफल +ΔDEF का क्षेत्रफल
+ΔDEF का क्षेत्रफल +ΔAEF का क्षेत्रफल
+ΔFBD का क्षेत्रफल +ΔCDE का क्षेत्रफल
=ΔABC का क्षेत्रफल
⇒ΔDEF का क्षेत्रफल =14×ΔABC का क्षेत्रफल
(iii) अब □BDEF का क्षेत्रफल =2×ΔDEF का क्षेत्रफल
=2×14×ΔABC का क्षेत्रफल
=12×ΔABC का क्षेत्रफल
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.4
Explore 8 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अतिलघु उत्तरीय प्रश्न
Explore 10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.2
Explore 6 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
Similar Questions
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionएक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
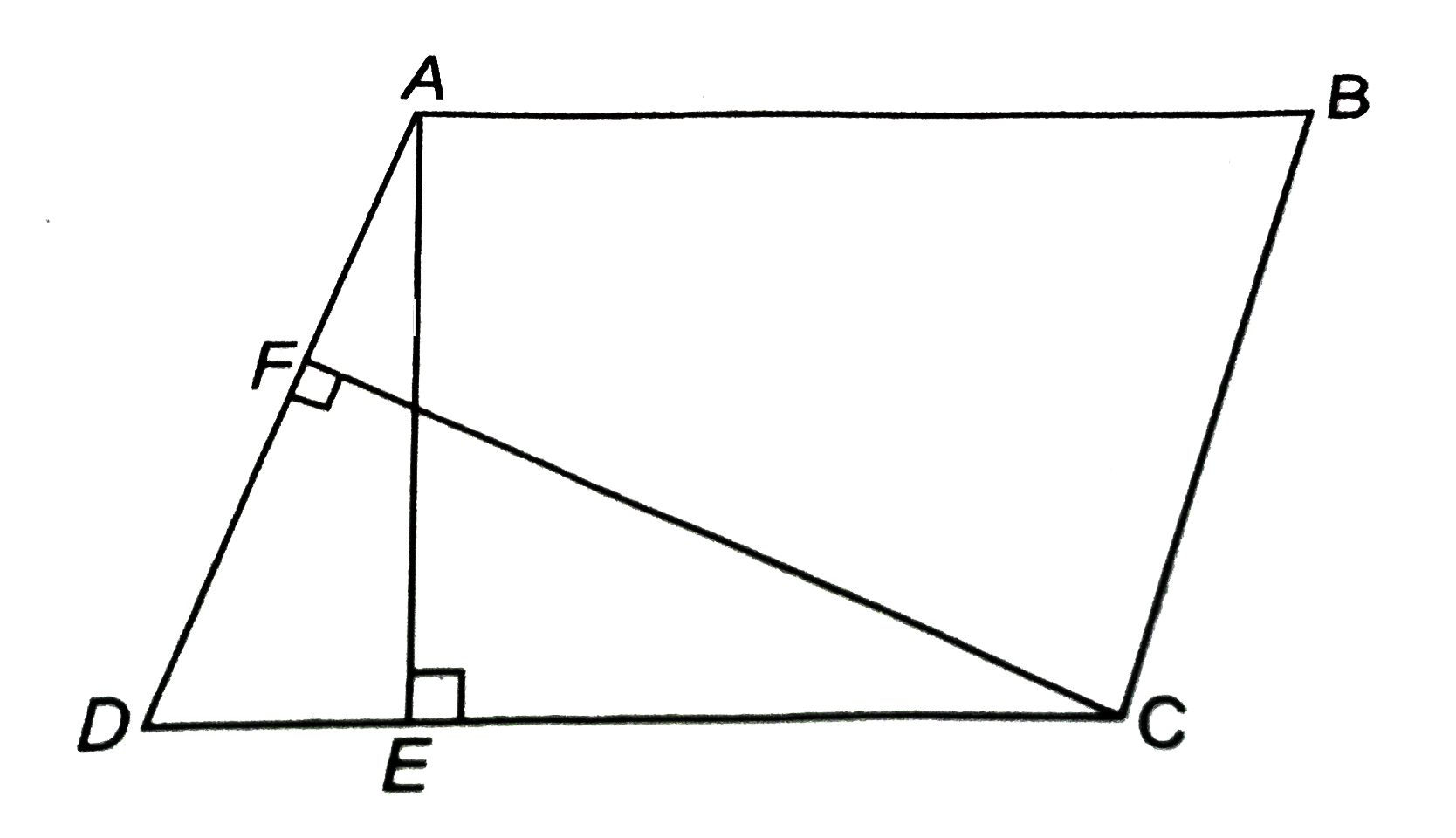
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
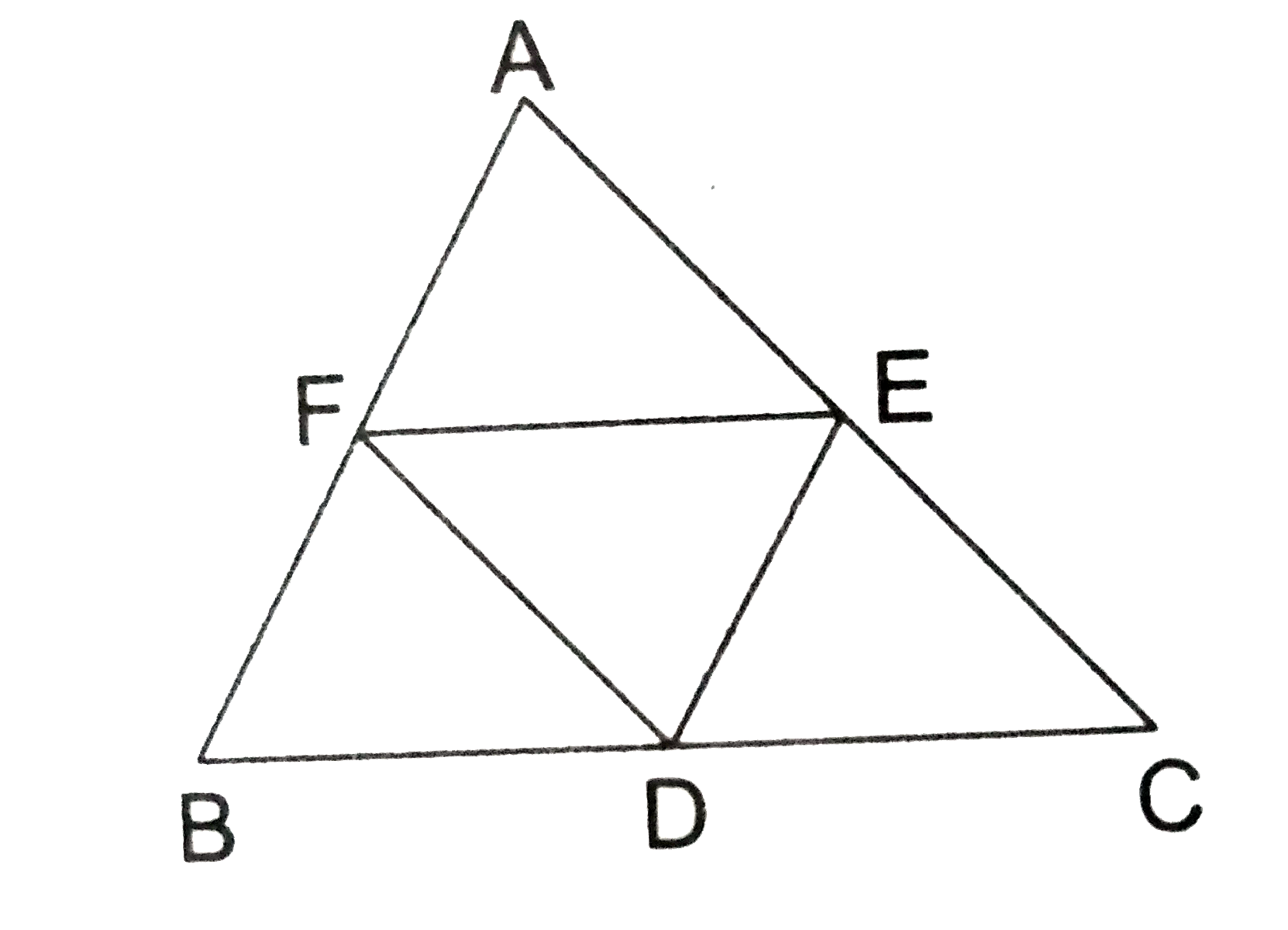
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि ABDE=BCEF=CAFD=25 तो ar(ΔABC):ar(ΔDEF)=
View SolutionD, E तथा F, ΔABC कि क्रमश : भुजाओ BC, CA तथा AB के मध्यबिंदु है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ΔABC के क्षेत्रफल का आधा है।
यह भी दिखाइए कि ar(DEF)=14ar(ABC).
View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
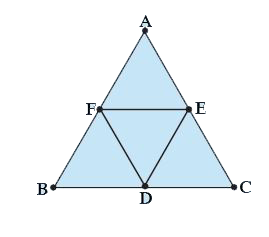
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
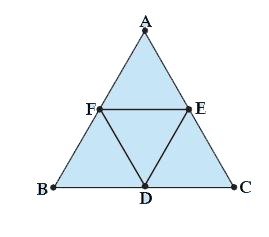
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View SolutionD, E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ BC,CA ਅਤੇ AB ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ।ਦਰਸਾਉ ਕਿ:- ar(BDEF)=12ar(ABC)
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View Solution

