XY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमशः E और F पर मिलती है, तो दर्शाइए कि :
ar(ABE) = ar(ACF)
∵ BE || AC⇒BE || YC …(1)
और BC || EY (दिया है) …(2)

∴□BCYE एक समान्तर चतुर्भुज है। (∵ सम्मुख भुजाओं के युग्म समान्तर है)
अब ΔABE और समान्तर चतुर्भुज BCYE समान आधार EB और समान समान्तर EB रेखाओं AC और के मध्य स्थित है।
∴ar(ΔABE)=12ar(||gm BCYE) ...(3)
अब, CF || AB⇒CF || BX और BC || XF (दिया है)
∴□BCFX एक समान्तर चतुर्भुज है (∵ सम्मुख भुजाओं के युग्म समान्तर है)
अब ΔACF और समान्तर चतुर्भुज BCFX समान आधार CF और समान समान्तर रेखाओं CF और AB के मध्य स्थित है।
∴ar(ΔACF)=12ar(||gm BCFX) ...(4)
परन्तु ar(||gm BCYE)=ar(BCFX) ...(5) (∵ समान्तर चतुर्भुज समान आधार BC और समान समान्तर रेखाओं BC और EF के मध्य स्थित है)
समीकरण (3), (4) और (5) से
ar(ΔABE)=ar(ΔACF)
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.4
Explore 8 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अतिलघु उत्तरीय प्रश्न
Explore 10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.2
Explore 6 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
Similar Questions
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionएक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
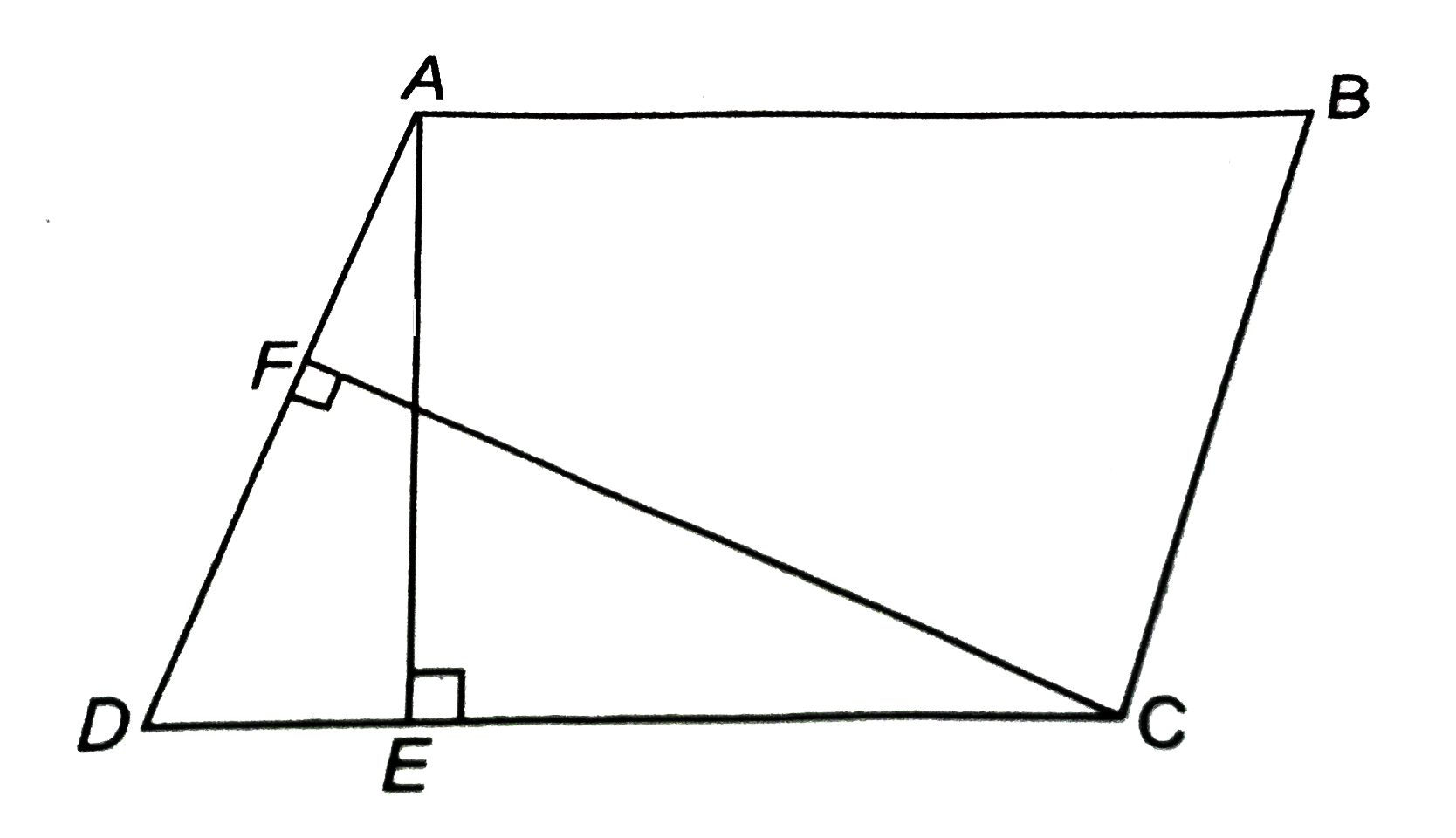
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionXY is a line parallel to side BC of a triangle ABC. If BF ||AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF)
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE||AC and CF ||AB meet XY at E and F respectively , show that ar(ABE)=ar(ACF)

View SolutionXY is a line parallel to side BC of triangle ABC. If BEIIAC and CFIIAB meet XY at E and F respectively,show that ar (ABE) = ar (ACF).
View SolutionXY ਤ੍ਰਿਭੁਜ ABC ਦੀ ਭੁਜਾ BC ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਹੈ। ਜੇਕਰ BE || AC ਅਤੇ CF || AB ਰੇਖਾ XY ਨੂੰ ਕ੍ਰਮਵਾਰ E ਅਤੇ F 'ਤੇ ਮਿਲਦੀ ਹੈ, ਤਾਂ ਦਰਸਾਓ ਕਿ:-ar (ABE) = ar (ACF)
View SolutionIn triangle ABC a straight line parallel to BC intersects AB and AC at D and E respectively. If AB = 2AD, then DE : BC is - त्रिभुज ABC में BC के समांतर एक सरल रेखा AB और AC को क्रमशः D और E पर काटती है । यदि AB= 2AD, तो DE : BC कितना होगा ।
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at the points P,Q and R respectively. If BP = 8.5 cm, CQ = 6.5 cm and AR = 4.5 cm, then the perimeter (in cm) of the △ABC is:
एक वृत्त किसी त्रिभुज ABC के भीतर स्थित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु P, Q और R पर स्पर्श करता है | यदि BP = 8.5 सेमी, CQ = 6.5 सेमी और AR = 4.5 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |
View SolutionA circle is inscribed in a triangle ABC. It touches sides AB, BC and AC at points P, Q and R respectively. If BP = 9cm, CQ = 10 cm and AR = 11 cm, then the perimeter (in cm) of the triangle ABC is :
एक वृत्त किसी त्रिभुज ABC के भीतर स्थित है | यह भुजाओं AB, BC और AC को क्रमशः P, Q और R पर स्पर्श करता है | यदि BP = 9 सेमी, CQ =10 सेमी और AR =11 सेमी है, तो त्रिभुज ABC का परिमाप ( सेमी में ) ज्ञात करें |
View Solution

