A light ray composed of two monochromatic components passes through a trihedral prism with refracting angle $θ = 60^{\circ}$ . Find the angle $Δ α$ between the components of the ray after its passage through the prism if their respective indies of refraction are equal to $1.515$ and $1.520$ . the prism is oriented to provide the least deflection angle.

Video Solution

Text Solution

Verified by Experts

From the Cauch's fromula and also experimetally the $R . I$ of a medium depends upon the wavelength o fthe mochromatic ray i.e., $n = f (λ)$ . In the case of least deviation of a monochromtic ray the passage a prism, we have:
$n \frac{sin (θ)}{2} = \frac{sin (α + θ)}{2}$ (1)
The above equation tales us that we have $n = n (α)$ , so we may write
$Δ n = \frac{d n}{d α} Δ α$ (2)
From Eqn. (1)
$d n sin . \frac{θ}{2} = \frac{1}{2} cos . \frac{α + θ}{2} d α$
or, $\frac{d n}{d α} = cos . \frac{\frac{α + θ}{2}}{2 sin . (\frac{θ}{2})}$ (3)
From Eqn (2) and (3)
$Δ n = cos . \frac{\frac{α + θ}{2}}{2 sin (\frac{θ}{2})} Δ α$
or, $Δ n = \frac{\sqrt{1 - {sin}^{2} (\frac{a + α}{2})}}{2 sin . (\frac{θ}{2})} δ α = \frac{\sqrt{1 - n^{2} {sin}^{2} (\frac{θ}{2})}}{2 sin (\frac{θ}{2})} Δ α$ (Using Eqn. 1)
Thus $Δ α = \frac{2 sin . (\frac{θ}{2})}{\sqrt{1 - n^{2} {sin}^{2} (\frac{θ}{2})}} Δ n = 0.44$

Updated on:21/07/2023

A trihedral prism with refracting angle $60^{\circ}$ deviates a light ray by $30^{\circ}$ . The refractive index of the material of prism
Amay be equal to $\sqrt{2}$
Bcan not be greater than $\sqrt{2}$
Ccan not be less than $\sqrt{2}$
Dnone of these
For a ray of light to pass symmetrically through a prism of refracting angle $60^{\circ} and n = 1.6,$ the angle of incidence is
A $36^{\circ}$
B $38^{\circ}$
C ${35.5}^{\circ}$
D $54^{\circ}$
A ray of light passes through a prism as shown in the figure.

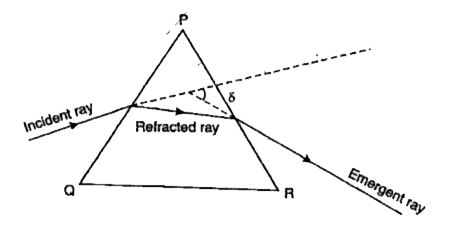
The angle $δ$ is known as
Aangle of deviation
Bangle of dispersion
Cangle of emergence
Dangle of refraction