A plane light wave falls normally on a diaphragm with round aperature opening the first N Fresnel zones for a point P on a screen located at a distance b form the diaphragm. The wavelength of light is equal to λ. Find the intensity of light I0 in front of the diaphragm if the distribution of intensity of light I(r) on the screen is knows. Here r is the distance from the point P.
The radius of the periphery of the Nth Fresnel zone is
rN√Nbλ
Then by conservation of energy
I0π(√Nbλ)=∫∞02πrdrI(r)
Here r is the distance from the point P.
Thus I0=2Nbλ∫∞0rdrI(r).
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Polarization Of Light
Explore 43 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Dispersion And Absorption Of Light
Explore 24 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Interference Of Light
Explore 33 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
A plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a=0.30mm (Fig.) A screen is placed at a distance b=110cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2.
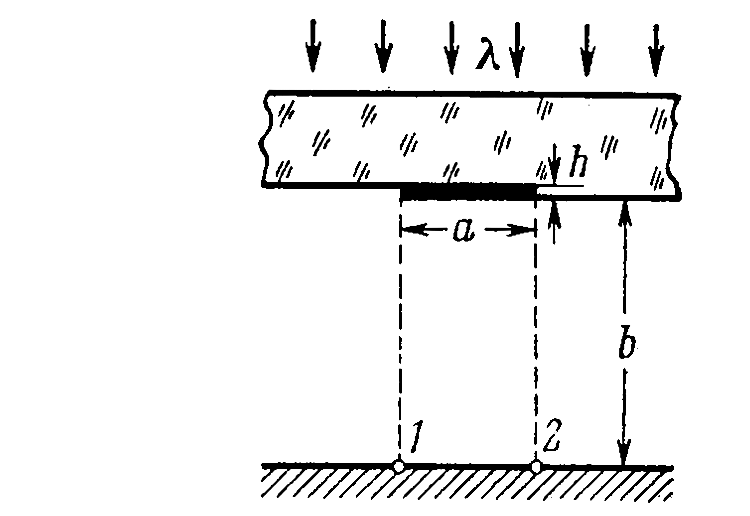
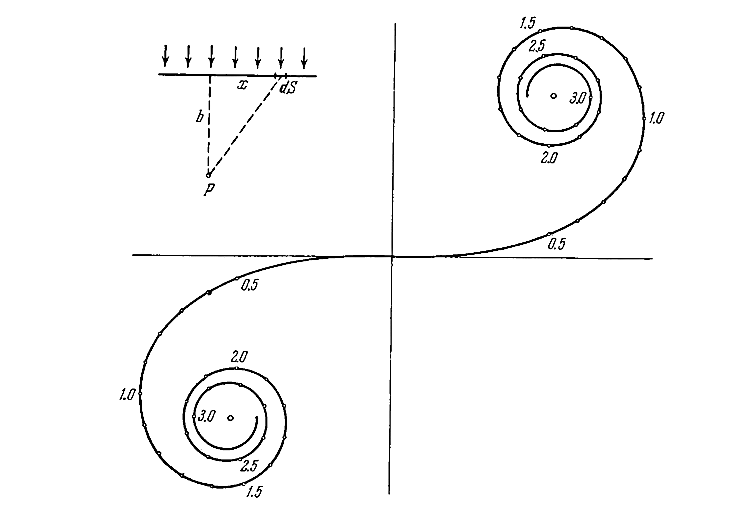
View SolutionSeparation between the slits in Young's double-slit experiment is d and screen is placed at a distance D from the slits to observe the interference pattern. Wavelength of light used is λ. Find the distance of point from centre of screen where intensity falls to (i) half the maximum and (ii) one-fourth of the maximum.
View Solution
Knowledge Check
In terms of wavelength of light (λ), intensity (I) of scattered light is related as
AI∝λ4BI∝u2CI∝1λ2DI∝1λ4If the distance between a point source and screen is doubled, then intensity of light on the screen will become
AFour timesBDoubleCHalfDOne-fourthIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is theintensity of central bright fringe, then intensity at distance from central maximum is
AIcos2(π2xdλD)BI2sin2(πxd2λD)CIcos2(πxdλD)DIsin2(πxdλD)
In the wave picture of light, intensity of light is determined by square of the amplitude of wave. What determines the intensity of light in the photon picture of light?
View SolutionPlane monochromatic light with intensity I0 falls normally on an opaque disc closing the first Fresnel zone for a point on the screen in front of the wave front. What would be the intensity I at the same point if (a) half of the disc along the diameter were removed, (b) half of the external half is removed along the the diameter ?
View SolutionIn Young's double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path diff. is λ is K units. Find the intensity of light at a point where path difference is λ/3.
View SolutionA plane monochromatic light wave falls normally on a diaphragm with two narrow slits separated by 2.5mm. The fringe pattern is formed on a screen 100 cm behind the diaphragm. By what distance will these fringes be displaced, when one of the slits is covered by a glass plate (μ=1.5) of thickness 10μm?
View SolutionIn young's double slit experiment using monochromatic light of wavelengths λ, the intensity of light at a point on the screen with path difference λ is M units. The intensity of light at a point where path difference is λ/3 is
View Solution

