A ray of light is incident on a prism of refracting angle A. if θC is the critical angle for the material of the prism with respect to the surrounding air, then:
An emergent ray will be there for all values of θC
An emergent ray will be there only for A≤2θC
A ray incident at an angle I can pass through the prism if sin>sin(A−θC)sinθC for θC<A<2θC
None of above is correct
To solve the problem, we need to analyze the behavior of light as it passes through a prism with a refracting angle A and a critical angle θC for the material of the prism with respect to air.
1. Understanding the Prism and Critical Angle:
- A prism has a refracting angle A.
- The critical angle θC is defined as the angle of incidence above which total internal reflection occurs when light travels from the prism to air.
2. Conditions for Emergent Ray:
- For light to emerge from the prism, the angle of incidence at the second surface (let's denote it as R2) must be less than the critical angle θC. If R2 is greater than θC, total internal reflection will occur, and no emergent ray will be produced.
3. Using the Minimum Deviation Condition:
- When the prism is at minimum deviation, the angles R1 and R2 are equal, and we can express this as:
R1+R2=A
Since R1=R2:
2R2=A⟹R2=A2
4. Condition for Emergence:
- For an emergent ray to exist, we need:
R2<θC
Substituting for R2:
A2<θC⟹A<2θC
- This means that if the refracting angle A is less than 2θC, an emergent ray will be present.
5. Conclusion:
- Based on the analysis, the correct condition for the emergence of the ray is that the refracting angle A must be less than 2θC.
Final Answer:
The emergent ray will be present if A<2θC.
- A prism has a refracting angle A.
- The critical angle θC is defined as the angle of incidence above which total internal reflection occurs when light travels from the prism to air.
- For light to emerge from the prism, the angle of incidence at the second surface (let's denote it as R2) must be less than the critical angle θC. If R2 is greater than θC, total internal reflection will occur, and no emergent ray will be produced.
- When the prism is at minimum deviation, the angles R1 and R2 are equal, and we can express this as:
R1+R2=A
Since R1=R2:
2R2=A⟹R2=A2
- For an emergent ray to exist, we need:
R2<θC
Substituting for R2:
A2<θC⟹A<2θC
- This means that if the refracting angle A is less than 2θC, an emergent ray will be present.
- Based on the analysis, the correct condition for the emergence of the ray is that the refracting angle A must be less than 2θC.
The emergent ray will be present if A<2θC.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Unsolved Numerical Problems
Explore 107 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Numerical MCQs Single Options Correct
Explore 51 Videos
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Unsolved Numberical Problems
Explore 73 Videos
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
Explore 82 Videos
Similar Questions
As shown in Fig. PQ is a ray incident on prism ABC. Show the corresponding refracted and emergent rays. The critical angle for the material of the prism is 45∘. What is refractive index of the material of prism ?
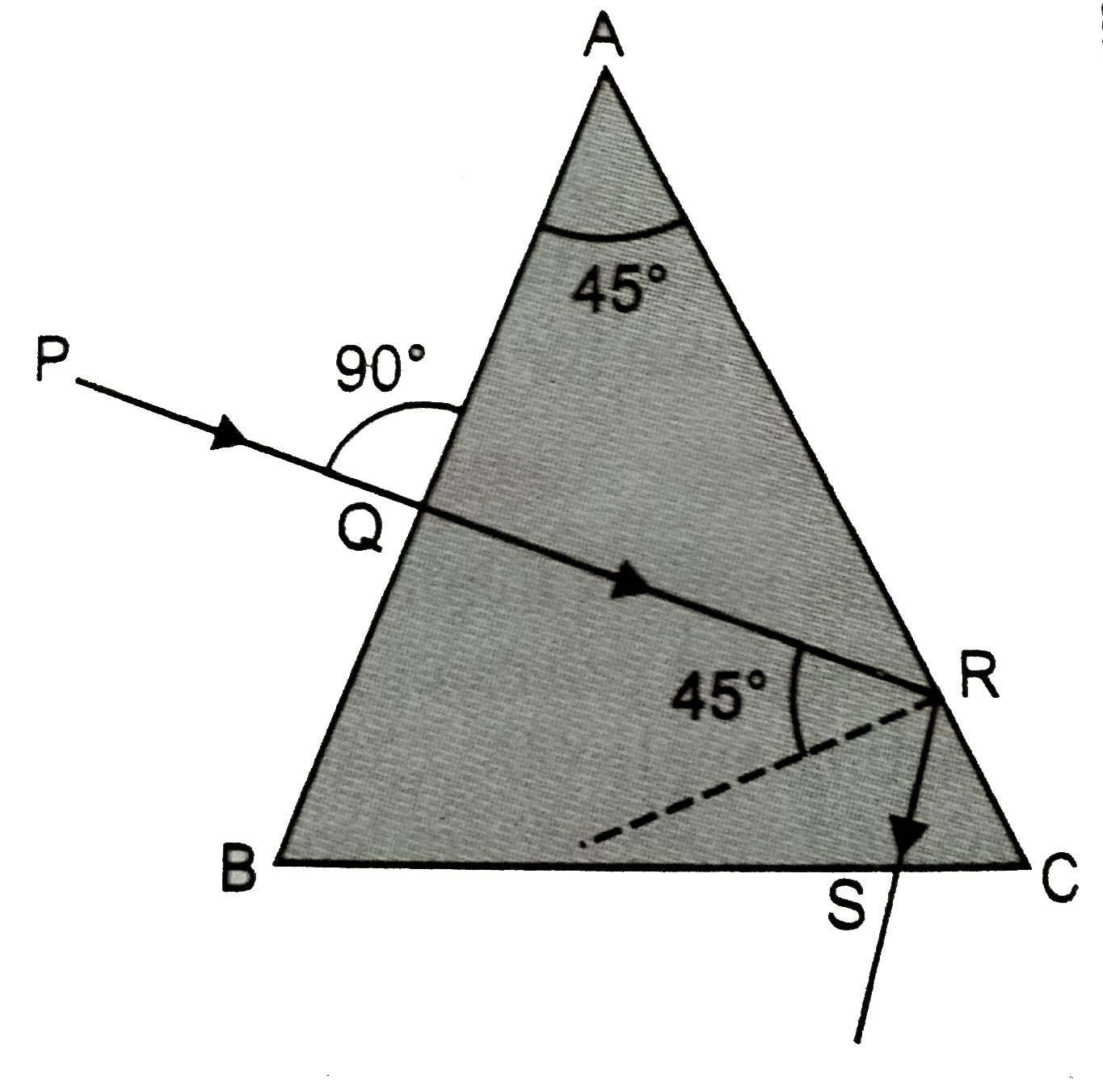 .
.
View SolutionA ray of light falls normally on one face of a prism of angle 45∘. If critical angle for material of the prism is 45∘, trace the course of rays, calculate μ.
View Solution
Knowledge Check
A prism can have a maximum refracting angle of (θC=critical angle for the material of prism )
A60∘BθCC2θCDslightly less than 180∘A prism can have a maximum refracting angle of (C = critical angle for the material of the prism)
A60∘BCC2CDslightly less than 180∘When a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
AEmerging ray is deviated by 30BEmerging ray is deviated by 45∘CEmerging ray just grazes the second refracting surfaceDThe ray undergoes total internal reflection at the second refracting surface
A ray of light is incident at an angle of 60∘ on the face of a prism with an angle of 60∘. Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
View SolutionA ray of light incident on a prism of angle 60∘, does not emerge out. Refractive index of material of prism may be
View SolutionA monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
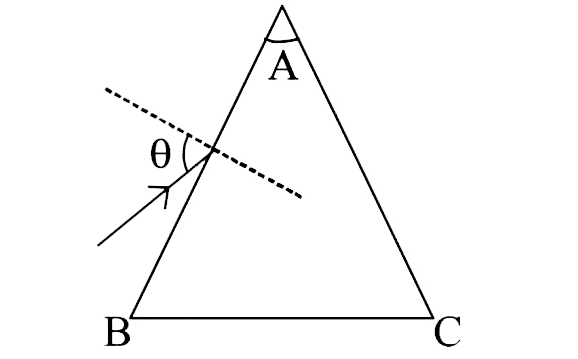
View SolutionA ray of light is incident on a refracting face of glass prism of refracting angle 30∘. If the ray emerges normally from the second refracting surface, the angle of incidence is refracting surface, the angle of incidence is
[aμg=1.5]
View Solution

