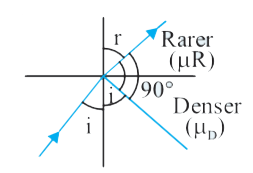
Two optical media have a plane boundary between them. Suppose θ1cr is the critical angle of incidence of a beam and θ1 is the angle of incidence at which the refracted beam is perpendicular to the reflected one (the beam is assumed to come from an optically denser medium). Find the relective index of these media if sinθ1cr/sinθ1=η=1.28.
Let two optical mediums of R.I.n1 an dn2 respectively be such that n1>n2. In the case when angle of incidence is θ1cr (Fig.) from the law of refraction
n1sinθ1cr=n2 (1)
In the case, when the angle o fincidence is θ1, from the law of refraction at the interface o fmediums 1 and 2.
n2sinθ1=n2sinθ2
But in accordance with the problem θ2=(π/2−θ1)
so, n1sinθ1=n2cosθ1(2)
Dividing Eqn (1) and (2)
sinθ1crsinθ1=1cosθ1
or, η=1cosθ1, so cosθ1=1η and sinθ1=√η2−1η (3)
But n1n2=cosθ1sinθ1
So, n1n2=1ηη√η2−1 (Using 3)
Thus n1n2=1√η2−1

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Knowledge Check
If θ1 and θ2 are the angles of incidence and reflection respectively, then correct relation between them is
Aθ1=π2+θ2Bθ1>θ2Cθ1<θ2Dθ1=θ2Light from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is θ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be
 Asin−1(cotθ)Bsin−1(tanθ)Csin−1(cosθ)Dsin−1(secθ)
Asin−1(cotθ)Bsin−1(tanθ)Csin−1(cosθ)Dsin−1(secθ)A beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is 51∘, the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is 43? [tan51∘=1.235]
A1.646B1.325C2.123D1.987
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i=tan−1(1/2). If the reflected and the refracted rays are mutually perpendicular to each-other, what is the value of the critical angle in degree?
View SolutionGiven √3tanθ=1andθ is an acute angle. Find the value of sin 3θ.
View SolutionIf θ is an acute angle and tanθ+secθ=1.5, find sinθ,tanθ and secθ.
View SolutionA light beam falls upon a plane-parallel glass plate d=6.0cm in thickness. The angle of incidence is θ=60∘. Find the value of deflection of the beam which passed through that plate.
View SolutionA paralel beam of monochromatic light is incident on a glass slab at an angle of incidentce 45∘. Find the ratio of width of beam in glass to that in air ( If refractive index of glass is 1.5).
View Solution
