Due to the external vertical force Fx=F0cosωt a body suspended by a spring performs forced steady − state oscillations according to the lawx=acos(ωt−φ). Find the work performed by the force F during one oscillation period.
The work doen in one cylcle is
A=∫Fdx=∫T0Fvdt=∫T0F0cosωt(−ωasin(ωt−φ))dt
=∫T0F0ωa(−cosωtsinωtcosφ+cos2ωtsinφ)dt
=12F0ωaT2sinφ=πaF0sinφ
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A ball of mass m suspended by a weightless spring can perform vertical oscillations with damping coefficient β. The natural oscillation frequency is equal to ω0. Due to the external vertical force varying as F=F0cosωt the ball performs steady − state harmonic oscillations. Find :
(a) the mean power (:P:) , develocped by the force F. averaged over one oscillations perod,
(b) the frequency ω of the force F at which (:P:) is maximum, what is (:P:)max equal to ?
View SolutionA uniform horizontal disc fixed at its centre to an elastic vertical rod performs forced torsional oscillations dur to the moment of forces Nz=Nmcosωt. The oscialltions obey the law φ=φmcos(ωt−α).
(a) the work performed by friction forces acting on the disc during one oscillation period ,
(b) the quality factor of the given oscillator if th emoment of inertia of the disc relative to the axis is equal to I.
View Solution
Knowledge Check
A point mass oscillates along the x−acis according to the law x=x0cos(ωt−π/4) if the acceleration of the particle is written as, a =Acos(ω+δ), then :
AA=x0,δ=−π/4BA=x0ω2,δ=−π/4CA=x0ω2,δ=−π/4DA=x0ω2,δ=3π/4A point mass oscillates along the x−acis according to the law x=x0cos(ωt−π/4) if the acceleration of the particle is written as, a =Acos(ω+δ), then :
AA=x0,δ=−π/4BA=x0ω2,δ=−π/4CA=x0ω2,δ=−π/4DA=x0ω2,δ=3π/4A point mass oscillates along the x-axis according to the law x=x0cos(moegat−π/4).Iftheae≤rationofthepartic≤iswrienasa=A cos(omegat+delta), the .
A(a) A=x0ω2,δ=3π/4B(b) A=x0,δ=−π/4C© A=x0ω2,δ=π/4D(d)A=x0ω2,δ=−π/4
A ball of mass m=50g is suspended by a weightless spring with stiffness x=20.0N/m. Due to external vertical harmonic force with frequency ω=25.0s−1 the ball performs steady − state oscillations with amplitude a=1.3cm. In this case the displacement of the ball lags in phase behind the external force by φ=34π. Find :
(a) the quality factor of the given oscillator ,
(b) the work performed by the external force during one oscillation period.
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
View SolutionA force F=a+b x acts on a particle in the X-direction, where a and b are constants. Find the work done by this force during a displacement from x=0 to x=d/
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
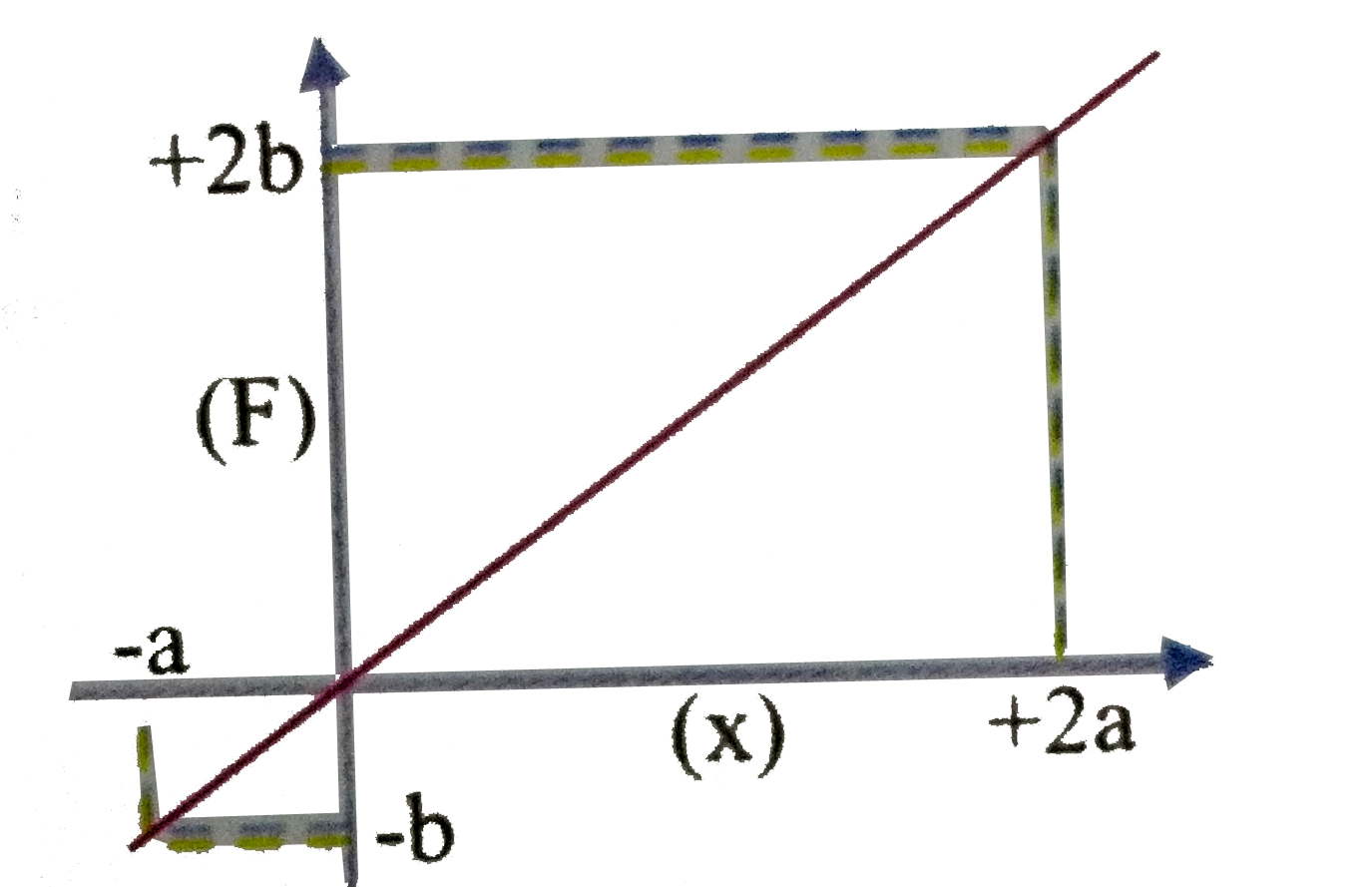 .
.
View Solution
