A mock− up of a CO2 molecule consists of three balls interconnected by identical light springs and placed along a straight line in the state of equilibrium. Such a system can freely perform oscillation of two types, as shown by the arrows in figure. Knowing the masses of the atomes, find the ration of frequencies of these oscillations
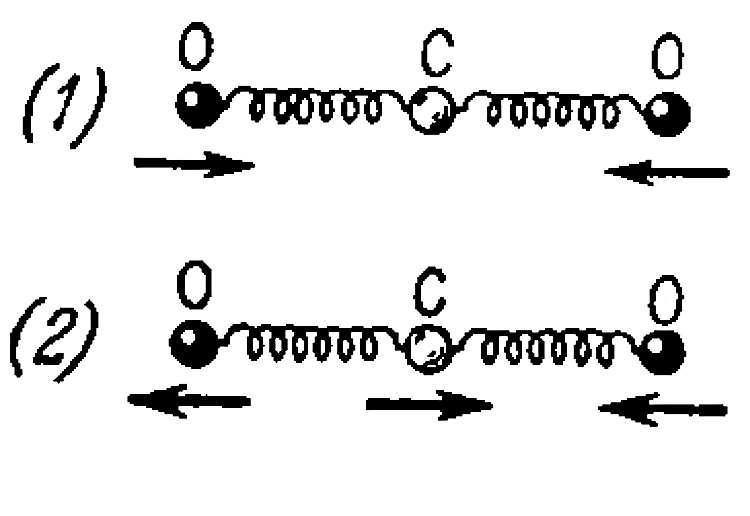
In the first mode the carbon atom remains fixed and the oxygent atoms move in equal & opposite steps. Then total energy is
(1) 122m0.x2+122kx2
where x is the displacement of one of the o atome ( say left one ). Thus
ω21=k/m0
(2)
In this mode the oxygen atoms move in equal steps in the same direction but the carbon atome moves in such a way as to keep the centre of mass fixed.
Thus 2m0x+mcy=0 or , y=−2m0mcx
K.E.=122m0.x2+12mc(2m0mc.x)2=122m0.x2+122m02m0mc.x2=122m0(1+2m0mc).x2
P.E.=12k(1+2m0mc)x2 +12k(1+2m0mc)2x2=122k(1+2m0mc)2x2
Thus ω22=km0(1+2m0mc and ω2=ω1√1+2m0mc
Hence, ω2=ω1√1+3212=ω1√113=1.91ω1


Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Two cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-
View SolutionA mock− up of a CO2 molecule consists of three balls interconnected by identical light springs and placed along a straight line in the state of equilibrium. Such a system can freely perform oscillation of two types, as shown by the arrows in figure. Knowing the masses of the atomes, find the ration of frequencies of these oscillations

View SolutionTwo identical springs S1andS2 are joined as shown in the figure. The oscillation frequency of the mass m is v. What will be the frequency of mass m, if one spring is removed ?

View SolutionAs shown in the figure a block of mass m is hung from the ceiling by the system of springs consisting of two layers. The force constant of each of the springs is k. The frequency of the vertical oscillations of the block is
View SolutionTwo identical small discs each of mass m placed on a frictionless horizontal floor are connected with the help of a light spring of force constant k. The discs are also connected with two light rods each of length 2√2m that are pivoted to a nail driven into the floor as shown as shown in the figure by a top view of the situation. If period of small oscillations of the system is 2π√(m/k), find relaxed length (in meters) of the spring.

View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View SolutionTwo balls with massesm1=1.0kg and m2=2.0kg are slipped on a thin smooth horizontal rod ( figure). The balls are interconnected by a light spring of stiffness x=24N/m. The left- hand ball is imparted the initial velocity v1=12cm/s. Find :
(a) the oscillation frequency of the system in the process of motion,
(b) the energy and the amplitude of oscillations

View SolutionTwo cubes with masses m1 and m2 were interconnected by a weightless spring of stiffness x and placed on a smooth horizontal surface. Then the cubes were drawn closer to each other and released simultaneously. Find the natural oscillation frequency of the system.
View SolutionIn the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
View Solution