Find the trajectory equation y(x) of a point if it moves according to the following laws :
(a) x=asinωt,y=asin2ωt,
(b) x=asinωt,y=acos2ωt.
Video Solution
Text Solution
From the Eqn. :x=asiniωt, we have
cosωt=√1−(x2/a2)
and from the Eqn. :y=asin2ωt
y=2asinωtcosωt=2x√1−(x2/a2) or y2=4x2(1−x2a2)
(b) From the Eqn. :x=asinωtt,
sin2ωt=x2/a2
From y=acos2ωt
y=a(1−2sin2ωt)=a(1−2x2a2)
For the plots see the plots of answer sheet of the problem book.
|
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Knowledge Check
The ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
A√2B1√2C1D2The displacement of a particle varies with time according to the relation y=asinωt+bcosωt.
AThe motion is oscillatory but not S.H.M.BThe motion is S.H.M. with amplitude a+bCThe motion is S.H.M. with amplitude a2+b2.DThe motion is S.H.M. with amplitude √a2+b2A particle moves in xy plane according to the law x = a sin ωtand y = a(1 – cosωt) where a and ω are constants. The particle traces
Aa parabolaBa straight line equallyinclined to x and y axesCa circleDa distance proportional to time
In y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
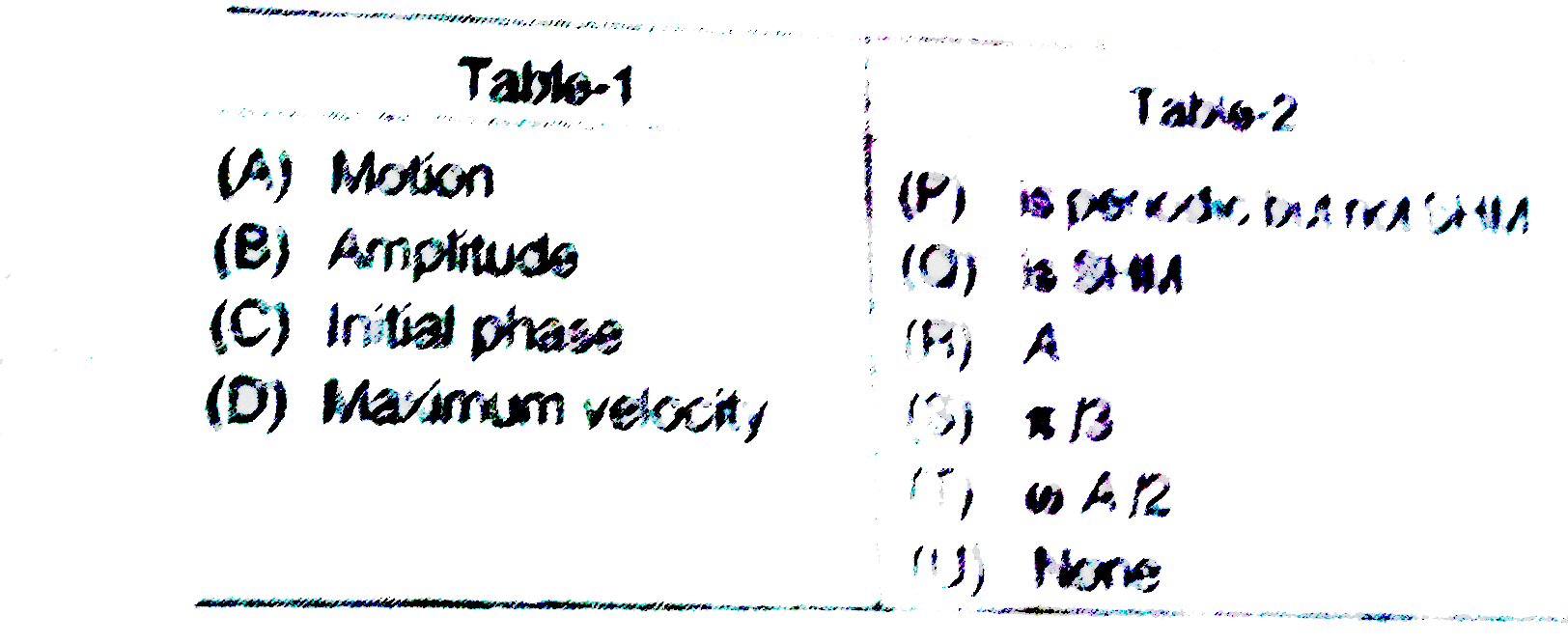
View SolutionWhat is the distance travelled by a point during the time oita if it moves in X−Y1plance,aord∈g→therelation<br>x= a sin omega t and y=a(1−cosωt)?
View SolutionIdentify which of the following function represent simple harmonic motion.
(i) Y=AeIωt (ii) Y=ae−ωt
(iii) y=asin2ωt (iv) y=asinωt+bcosωt
(v) y=sinωt+bcos2ωt
View SolutionWhich two of the following waves are in the same phase?
y=Asin(kx−ωt)
y=Asin(kx−ωt+π)
y=Asin(kx−ωt+π/2)
y=Asin(kx−ωt+2π)
View SolutionFind the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
View Solution

