A particle performs harmonic oscillations along the x axis about the equilibrium position x=0. The oscillation frequency is ω=4.00s−1. At a certain moment of time the particle has a coordinatex0=25.0cm and its velocity is equal to vx0=100cm/s.
Find the coordinate x and the velocity vx of the particle t=2.40s after that moment.
Let the general equationof S.H.M. be
x=acos(ωt+α)………..(1)
So, vx=−asin(ωt+α)……(2)
Let us assume that at t=0,x=x0 and vx=vx0.
Therefore tanα=−vx0ωx0 and a=√x20+(vx0ω)2=35.35cm
Under our assumption Equns (1) and (2) give the sought x and vx if
t=t=2.40s,a=√x20+(vx0/ω)2 and α=tan−1(−vxωx0)=−π4
Putting all the given numberical values, we get :
x=−29cmand vx=−81cm/s
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View Solution
Knowledge Check
A particle moves along the positive x-axis with an accelerationax which increases linearly with x, as shown in the graph. If the velocity of the particle at x=4cm is 0.40m/s determine the velocity at x=12cm
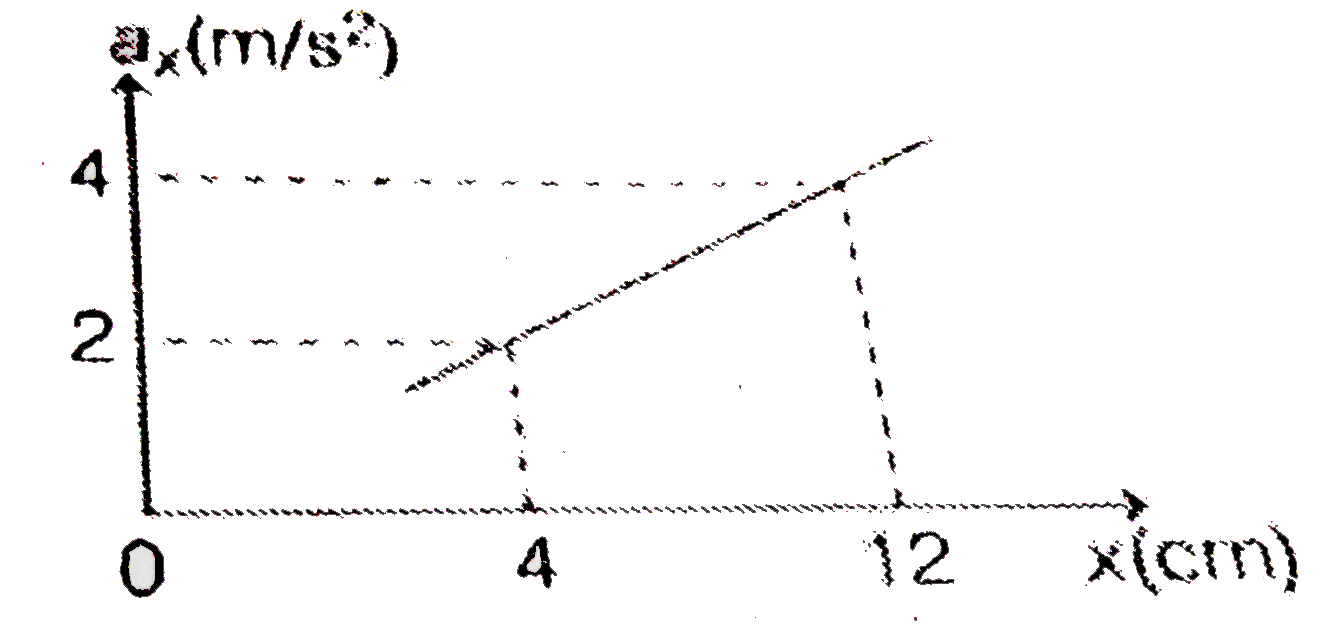 A0.2m/sB0.4m/sC0.8m/sD1.6m/s
A0.2m/sB0.4m/sC0.8m/sD1.6m/sA particle moving along the x axis has a position given by x=54t−2.0t3m. At the time t=3.0s, the speed of the particle is zero. Which statement is correct ?
A4.3×104m/s2, southB9.4×104m/s2, northC5.1×104m/s2, northD2.2×103m/s2, southA particle moves along x-axis. At time t=0, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its (speed)2 versus its x-coordinate is as shown in graph.

The time at which velocity of particle is zero.At=5secBt=20secCt=5√2secDt=20√2sec
At the moment t=0 a particle starts moving along the x axis so that its velocity projection varies as vx=35cosπtcm/s, where t is expressed in seconds. Find the distance that this particle covers during t=2.80s after the start.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionA point performs damped oscilaltions with frequency ω and dampled coefficient β. Find the velocity amplitude of the point as a function of time t if at the moment t=0
(a) its displacement amplitude is equal to a0,
(b) the displacement of the point x(0)=0 and its velocity projection vx(0)=.x0
View SolutionWhat is the oscillation amplitude of a 4.00kg box oscillating on a spring with spring constant 100N/m if at time t= 1.00s the position is x = 0.129m and the velocity is v= 5.00m/s? At t= 0, what are (a) the position and (b) the velocity?
View SolutionA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
View Solution

