The space between the plates of a parallel-plate capacitor is filled consecutively with two dielectric layers 1 and 2 having the thickness of d1 and d2 and the permittivities esπlon1 and esπlon2 respectively. The area of each plate is equal to S. Find :
(a) As it is series combination of two capacitors,
1C=d1ε0ε1S+d2ε0ε2S or, C=ε0S(d1/ε1)+(d2/ε2)
(b) Let, σ be the initial surface charge density, then density of bound charge on the boundary plane,
σ'=σ(1−1ε1)−σ(1−1ε2)=σ(1ε2−1ε1)
But, σ=qS=CVS=ε0Sε1ε2ε2d1+ε1d2VS
So, σ'=ε0V(ε1−ε2)ε2d1+ε1d2

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Current
Explore 72 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Conductors And Dielectrics In An Electric Field
Explore 47 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
The space between the plates of a parallel plate capacitor is filled conseutively with two dielectric layers fo thickness d1andd2 having relative permittvities ∈1and∈2 respectively. If A is area of each plate, what is the capacity of the capacitor ?
View SolutionThe gap between the plates of a prallel-plate capacitor is filled up with two dielectric layers 1 and 2 thickness d1 and d2 permittivities ε1 and ε2 and resistivities ρ1 and ρ2. A dc voltage V is applied to the capacitor with electric field directed from layer 1 to layer 2 find σ the surface density of extraneous charges at the boundary between the dielectric layers and the condition under with σ=0.
View Solution
Knowledge Check
If the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
AIncreases by a factor 2BIncreases by a factor √2CDecreased by a factor √2DDecreased by a factor 1/2In figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A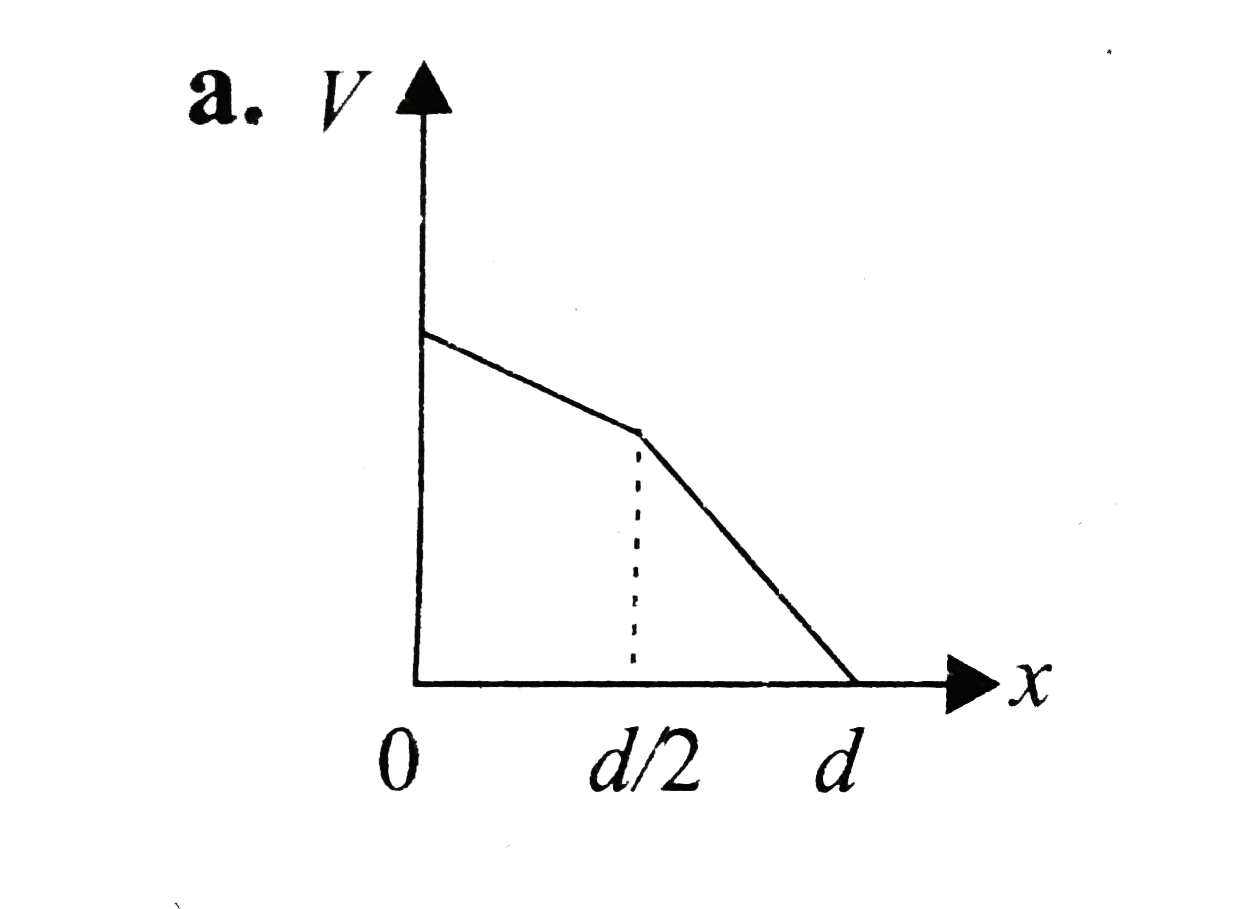 B
B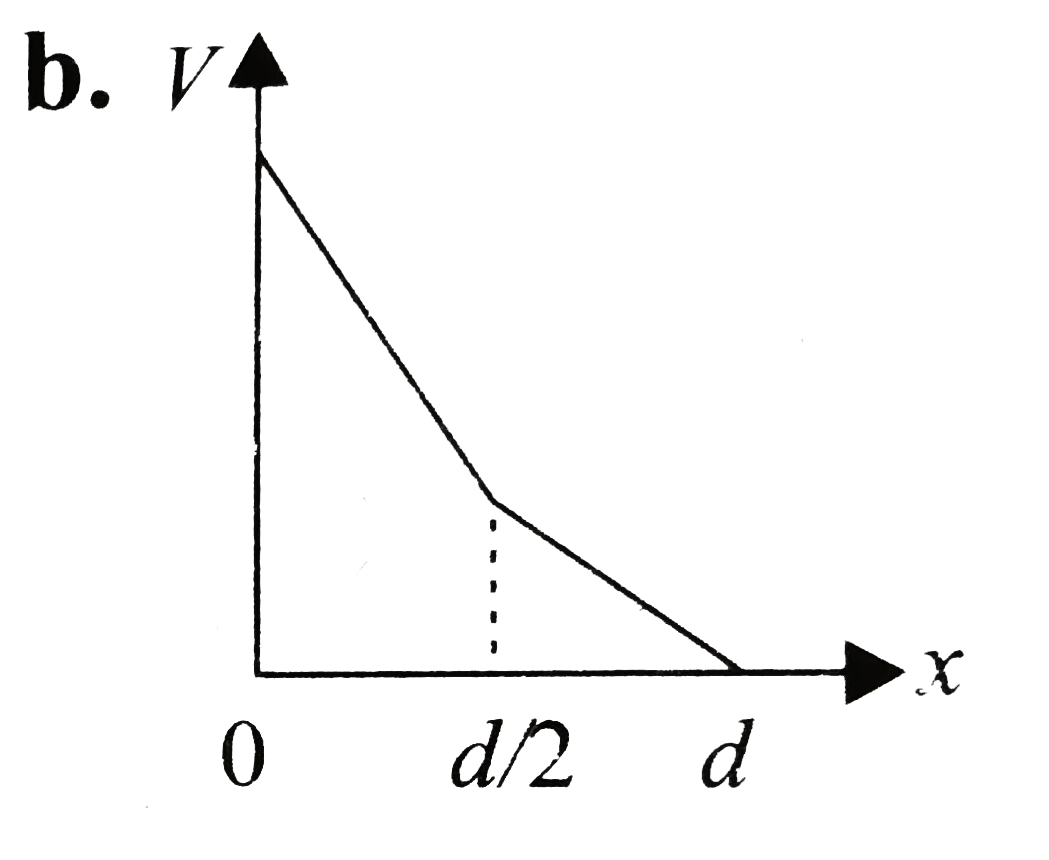 C
C D
D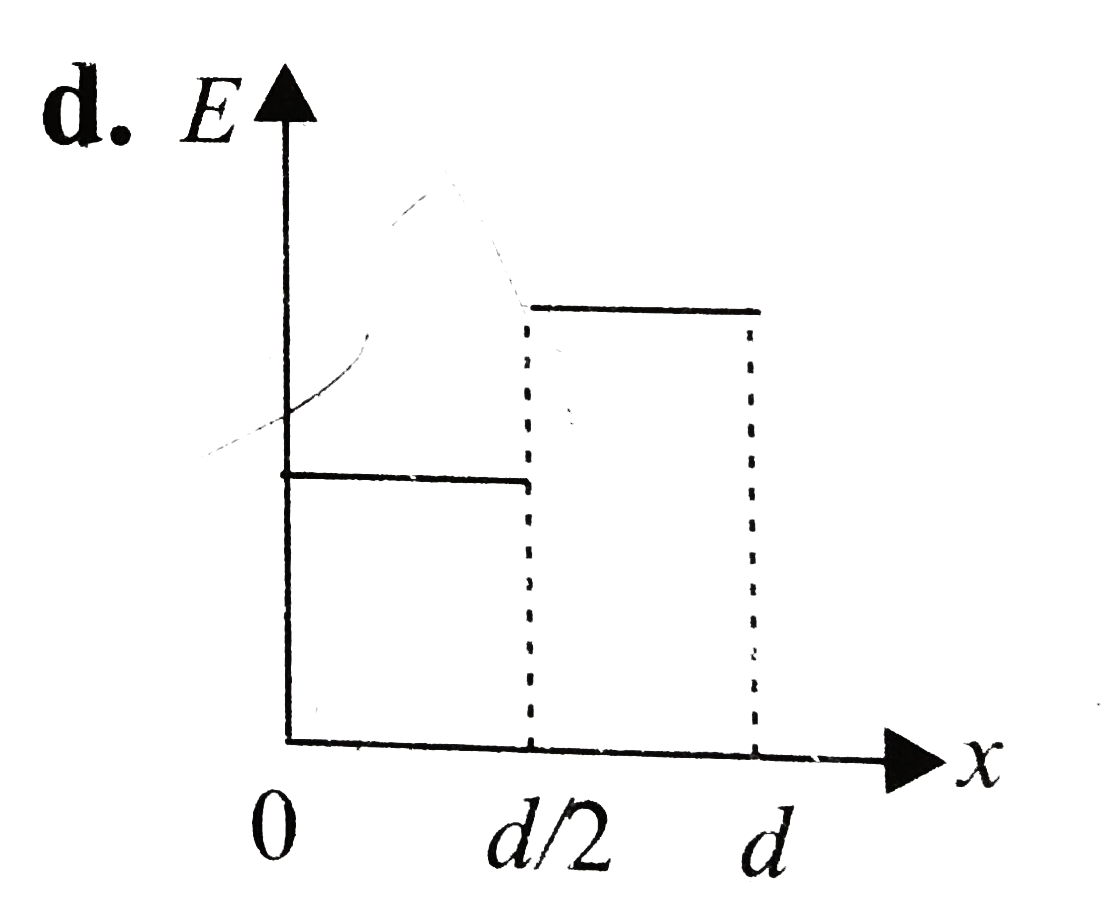
The separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
Aε0Ad−x(1−1K)Bε0Ad+x(1−1K)Cε0Ad+x(1+1K)Dε0Ad−x(1+2K)
The gap between the plates of a parallel-plate capacitor is filled with istropic dielectrc whose permittlvity ε varies linearly from esπlon1 to ε2(ε2>ε1) in the direction perpendicular to the plates. The area of each plate equals S, the separation between the plates is equal to d. Find :
(a) the capacitance of the capacitor,
(b) the space density of the bound chagres as a function of a if the charge of the capacitor is q and E in it is directed toward the growing ε values.
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionWhen the space between the plates of a parallel plate condenser is completely filled with two slabs of dielectric constants K1 and K2 and each slab having area A and thickness equal to d2 as shown in the figure

Fig. The equivalent circuit is as shown.
 .
.
View Solution

