An ideal gas goes through a polytropic process with exponent n. Find the mean free path λ and the number of collisions of each molecule per second v as a function of
(a) the volume V ,
(b) the pressure p ,
( c) the temperature T.
In the polytropic process of index n
pVn= constant, TVn−1= constant and p1−nTn= constant
(a) λαV
vαT1/2V=V1−n2V−1=V−n+12
(b) λαTp,Tnαpn−1 or Tαp1−1n
so λαp−1/n
v=<v>λαp√Tαp1−12+12n=pn+12n
( c) λαTp,pαTnn−1
λαT1−nn1=T−1n−1=T11−n
vαp√TαTnn−1−12=Tn+12(n−1).
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Phase Transformations
Explore 35 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
An ideal gas consisting of rigid diatimic molecules goes through an adiabatic process process. How do the mean free path λ and the number of collisions of each molecule per second v depend in this process on
(a) the volumeV ,
(b) the pressure p ,
( c) the temperature T ?
View SolutionHow does the mean free path λ and the number of collisions of each molecule per unit time v depend on the absolute temperature of an ideal gas undergoing
(a) an isochoric process ,
(b) an isobaric process ?
View Solution
Knowledge Check
Which of the following represents the mean free path for a gas ? (where n is number of gas molecules per unit volume, d is diameter of gas molecules)
A1√2πmB1√2πnd2C1√2πnd3D1√2πnd3/2P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
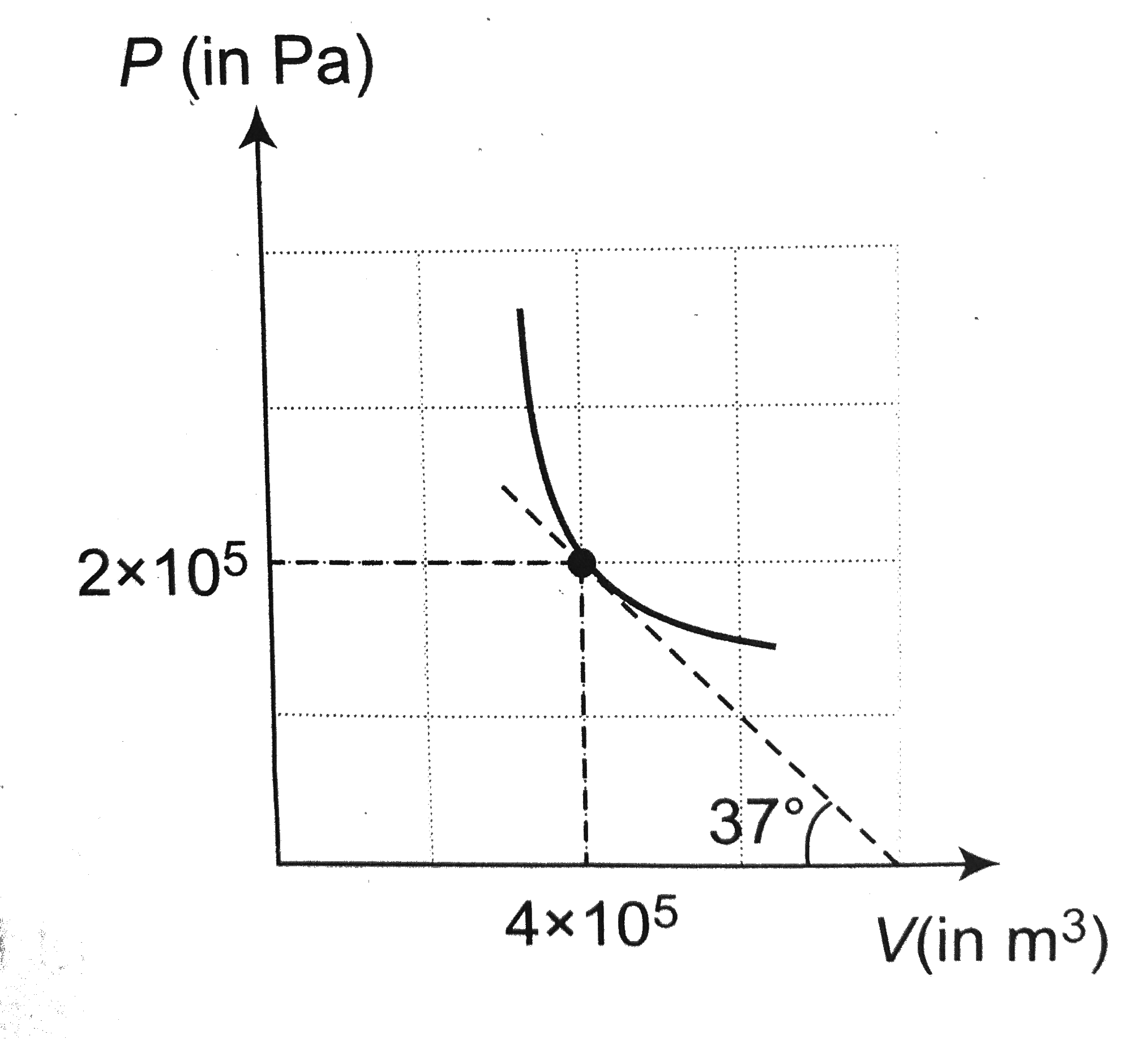 A34B−32C53D32
A34B−32C53D32The expression for mean free path (λ) of molecules is given by [where n is no of molecules per unit volume and d molecular diameter of the gas]
A√2πnd2B1pnd2C1√2πnd2D1√2πnd
As a result of some process the pressure of an ideal gas increases n−fold. How many times have the mean free path λ and the number of collisions of each molecule per unit time v changed and how, if the process is
(a) isochoric ,
(b) isothermal ?
View SolutionAn ideal gas goes through a polytropic process. Find the polytropic exponent n if in this process the coefficient
(a) of diffusion ,
(b) of viscosity ,
( c) of heat conductivity remains constant.
View SolutionDetermine the molar heat capacity of a polytropic process through which an ideal gas consisting of rigid diatomic molecules goes and in which the number of collisions between the molecules remains constant
(a) in a unit volume ,
(b) in the total volume of the gas.
View SolutionIn a dilute gas at pressure P and temperature T, the mean time between successive collisions of a molecule varies with T as :
View SolutionIf V is the molecular speed and / is the mean free path of molecule of gas, then the collision frequency is" "[2010]
View Solution

