A cylinder rolls without slipping over a horizontal plane. The radius of the cylinder is equal to r. Find the curvature radii of trajectories traced out by the points A and B(see figure)

Let us draw the kinematic diagram of the rolling cylinder on the basis of the solution of problem 1.53.


As, an arbitrary point of the cylinder follows a curve, its normal acceleration and radius of curvature are related by the well known equation
wn=v2R
so, for point A, wA(n)=v2ARA
or, RA=4v2cω2r=4r (because vc=ωr, for pure rolling)
Similarly for point B,
wB(n)=v2BRB
ω2rcos45∘=(√2vc)2RB,
RB=2√2v2Cω2r=2√2r
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Knowledge Check
A cylinder rolls without slipping down an inclined plane, the number of degrees of freedom it has, is
A2B3C5D1A solid cylinder rolls without slipping down an inclined plane of height h. The velocity of the cylinder when it reaches the bouom is
A√2gh3B√4gh3C√3gh2D√ghA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2
If a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45° then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination '0' then the minimum coefficient of friction required to support pure rolling is
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View SolutionA cylinder is rolling without sliding over two horizontal planks (surfaces) 1 and 2. If the velocities of the surfaces A and B are −vˆi and 2vˆi respectively, find the:
a. Position of instantaneous axis of rotation.
b. Angular velocity of the cylinder.
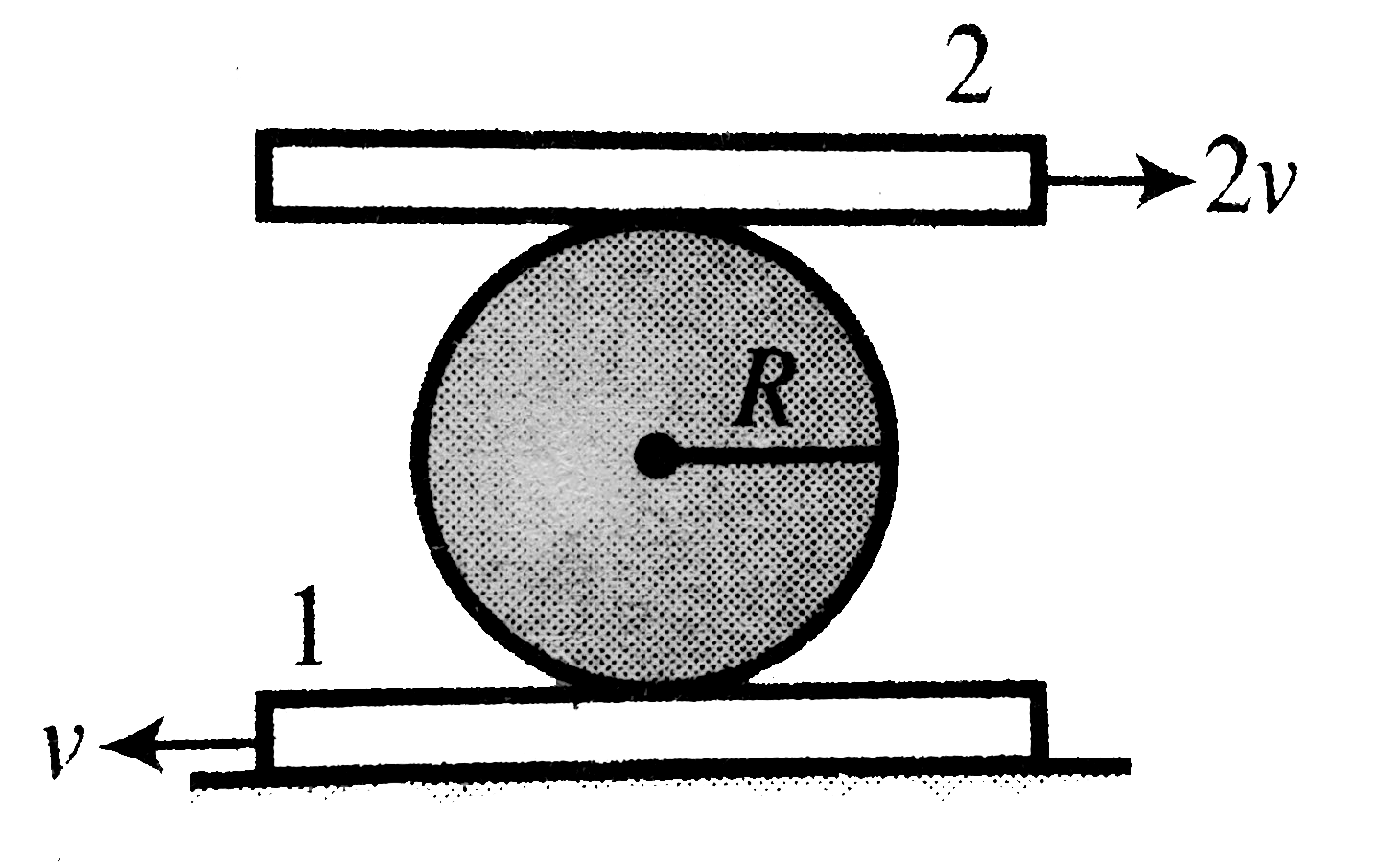
View Solution


