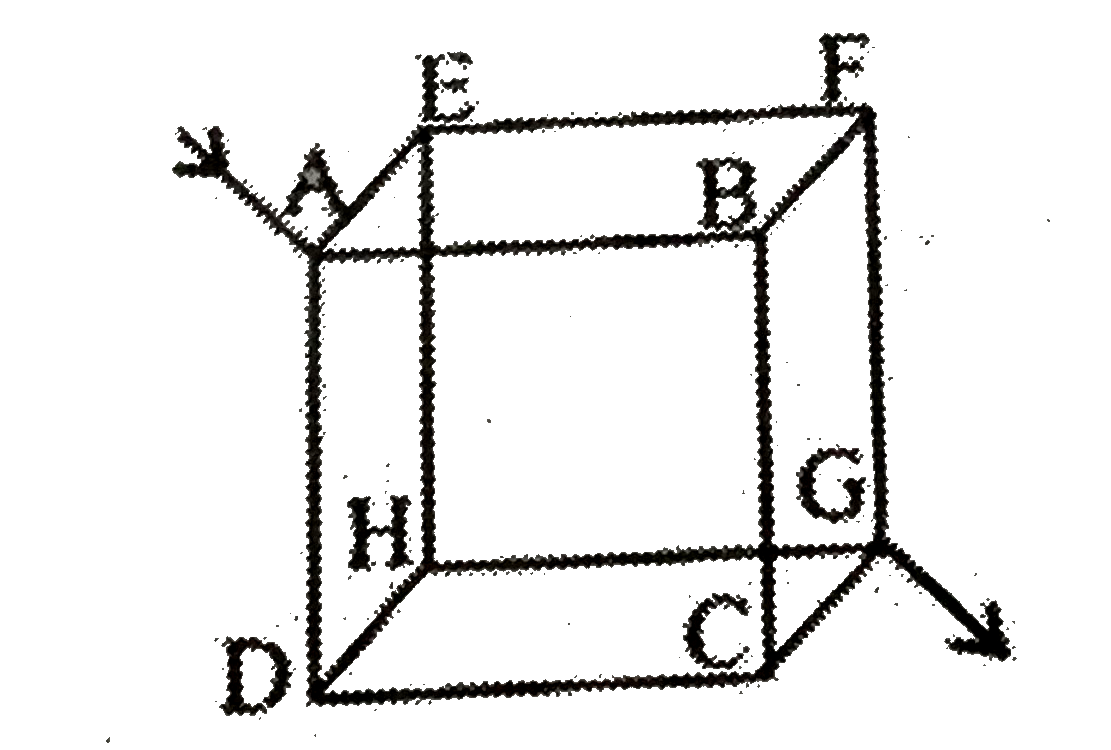
Twelve identical wires each of resistance 6Ω are arranged to from a skelence cube. A current of 40mA is led cube at the current and out at the diagonally opposite corner. Calculate the potential difference development across these current and the effective resistance of the network
The correct Answer is:0.2V
Follow example 10 the effective resistance between two two point , which are diagonally opposite cornes of a skellon cube of 12 wires
=5r/6=5×6/6=5Ω
pot diff developed = resistance x current
5×(40×10−3)=0.2V
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Jee (main and advance)
Explore 4 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Interger Type
Explore 2 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Value based
Explore 2 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Knowledge Check
Twelve wires each of resistance 6Ω are connected to from a cube as shown in the adjoining figure. The current enters at a cornet A and leaves at erhe diagonally opposite corner G. The equivalent resistance across the corners A and G is
 A12ΩB6ΩC3ΩD5Ω
A12ΩB6ΩC3ΩD5ΩTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4ATwelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
A712rB127rC57rD125r
A current of 0.2A flows through a conductor of resistance 4.5Ω. Calculate the potential difference at the ends of the conductor.
View SolutionThree identical cells, each of emf 2V and internal resistance 0.2 ohm, are connected in series to an external resistor of 7.4 ohm. Calculate the current in the circuit and the terminal potential difference across an equivalent.
View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionA regular hexagon is formed by six wires each of resistance rΩ and the corners are joined to the center by wires of the same resistance. If the current enters at one corner and leaves at the opposite corner, find the equivalent resistance of the conductor.
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View Solution

