A wire of resistance 2.20Ω has a length 2m. Calculate the length of the similar wire which connected in parallel with 2m length wire will give a resistance of 2.0Ω
The correct Answer is:20m
To solve the problem, we need to find the length of a similar wire that, when connected in parallel with a 2-meter wire of resistance 2.20 Ω, results in a total resistance of 2.0 Ω.
1. Identify Given Values:
- Resistance of the first wire (R1) = 2.20 Ω
- Length of the first wire (L1) = 2 m
- Desired total resistance (R_total) = 2.0 Ω
2. Calculate the Resistance per Unit Length:
The resistance per unit length (R_per_unit_length) can be calculated using the formula:
Rper unit length=R1L1
Substituting the known values:
Rper unit length=2.20Ω2m=1.1Ω/m
3. Use the Formula for Parallel Resistance:
When two resistors (R1 and R2) are in parallel, the total resistance (R_total) can be calculated using the formula:
1Rtotal=1R1+1R2
Here, R2 is the resistance of the second wire, which we need to find.
4. Express R2 in Terms of Length:
The resistance of the second wire (R2) can be expressed in terms of its length (L2):
R2=Rper unit length×L2=1.1Ω/m×L2
5. Substitute R1 and R2 into the Parallel Resistance Formula:
Substitute R1 and R2 into the parallel resistance formula:
12.0=12.20+11.1×L2
6. Solve for L2:
Rearranging the equation gives:
11.1×L2=12.0−12.20
Finding a common denominator for the right-hand side:
12.0=1122,12.20=1022
So,
11.1×L2=11−1022=122
Therefore,
1.1×L2=22⇒L2=221.1=20m
Final Answer:
The length of the similar wire (L2) that needs to be connected in parallel is 20 meters.
---
- Resistance of the first wire (R1) = 2.20 Ω
- Length of the first wire (L1) = 2 m
- Desired total resistance (R_total) = 2.0 Ω
The resistance per unit length (R_per_unit_length) can be calculated using the formula:
Rper unit length=R1L1
Substituting the known values:
Rper unit length=2.20Ω2m=1.1Ω/m
When two resistors (R1 and R2) are in parallel, the total resistance (R_total) can be calculated using the formula:
1Rtotal=1R1+1R2
Here, R2 is the resistance of the second wire, which we need to find.
The resistance of the second wire (R2) can be expressed in terms of its length (L2):
R2=Rper unit length×L2=1.1Ω/m×L2
Substitute R1 and R2 into the parallel resistance formula:
12.0=12.20+11.1×L2
Rearranging the equation gives:
11.1×L2=12.0−12.20
Finding a common denominator for the right-hand side:
12.0=1122,12.20=1022
So,
11.1×L2=11−1022=122
Therefore,
1.1×L2=22⇒L2=221.1=20m
The length of the similar wire (L2) that needs to be connected in parallel is 20 meters.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
The specific resistance of a wire is ρ, its volume is 3m3 and its resistance is 3ohms, then its length will be
A√1/ρB3/√ρC√3/ρDρ/√3A 10 m long wire of uniform cross section and 20Ω resistance is used in a potentiometer. The wire is connected in series with a battery of 5 V along with an external resistance of 480Ω . If an unknown emf E is balanced at 6.0 m length of the wire, then the value of unknown emf is:
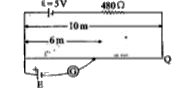 A1.2VB1.02VC0.2VD0.12V
A1.2VB1.02VC0.2VD0.12VA wire of length 3 m connected in the left gap of a metre bridge balances a 8Ω resistance in the right gap at a point, which divides the bridge wire in the ratio of 3:2 . What is the length of the wire corresponding to a resistance of the length of the wire corresponding to a resistance of 1Ω ?
A1mB0.75 mC0.5 mD0.25 m
What should be the length of a nichrome wire of resistance 4.5Ω, if the length of a similar wire is 60cm and resistance 2.5Ω ?
View SolutionA piece of wire of resistance 20Ω is drawn so that its length is increased to twice is original length. Calculate resistance of the wire in the new situation.
View SolutionA 10 m long wire of uniform cross section and 20 Ω resistance is used in a potentiometer. The wire is connected in series with a battery of 5 V along with an external resistance of 480 Ω. If and unknown emf E is balanced at 6.0 m length of the wire,then the value of unknown emf is
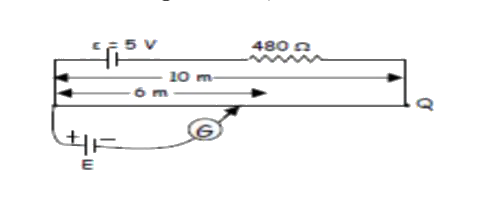
View SolutionCalculate the resistivity of the material of a wire 1.0 m long, 0.4 mm diameter and having a resistance of 2.0Ω.
View SolutionA wire has a resistance of 16Ω. It is melted and drawn into a wire of half its length. Calculate the resistance of the new wire. What is the percentage change in its resistance ?
View Solution