A d.c. voltage with appreciable ripple expressed as V=V1+V2cosωt is applied is a resistor The amount of heat generated per second is given by
V21+V222R
2V21+V222R
V21+2V222R
none of the above
The correct Answer is:b
Heat generated per sec
H=V2R=(V1+V2cosωt)2R
=V21+V22cos2ωt+2V1V2cosωtR
Average value of cos2ωt over a cycle =12
Average value of cosωt over a cycle =0
∴ Heat generated per second,
H=V21+V22×12+2V1V2×0R=2V21+V222R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
A resistor of resistance 200 Ω is connected to an AC source represented as V = (20V) sin (250πs−1)t. Find the amount of heat dissipated across resistor in the time interval 0 to 1 ms .
View SolutionIn the given circuit, one of the capacitors was connected to a voltage V0 and then at the moment t=0 was shorted by means of the switch. Find the amount of heat generated.
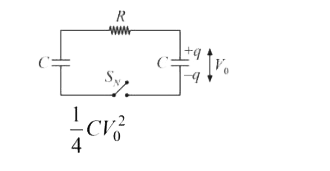
View Solution
Knowledge Check
A d.c. voltage with appreciable riple expressed as V=V1+V2cosωt is applied to a resistor R. The amount of heat generated per second is given by -
AV21+V222RB2V21+V222RCV21+2V222RDNone of theseWhen a voltage V=V0 cos ωt is applied across a resistor of resistance R, the average power dissipated per cycle in the resistor is given by
AV0√2RBV0√2ωRCV202RDV202ωR220 V, 50 Hz , AC is applied to a resistor . The instantaneous value of voltage is
A220√2sin100πtB220sin100πtC220√2sin50πtD220sin50πt
The voltage supplied to a circuit is given by V=V0t32, where t is time in second. Find the rms value of voltage for the period, t=0 to t=1s.
View SolutionOne mole of an ideal gas with heat capacity at constant pressure C_(P) undergoes the process T=T_(0)+alpha V where T_(0) and a are constants.If its volume increases from V_(1)toV_(2) the amount of heat transferred to the gas is C_(P)RT_(0)ln((V_(2))/(V_(1))) alpha C_(P)((V_(2)-V_(1)))/(RT_(0))ln((V_(2))/(V_(1))) alpha C_(P)(V_(2)-V_(1))+RT_(0)ln((V_(2))/(V_(1)))
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionA small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionA coil of wire of resistance 50Ω is embedded in a block of ice. If a potential difference of 210 V is applied across the coil, the amount of ice melted per second will be
View Solution
