A long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by ρ=cr2, where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.
To find the resistance per unit length of a long cylindrical conductor with a varying resistivity, we will follow these steps:
Step 1: Understanding the Geometry and Resistivity
We have a long cylindrical conductor with a radius a and a cross-sectional area A. The resistivity ρ of the material is given by:
ρ=cr2
where c is a constant and r is the distance from the axis of the cylinder.
Step 2: Setting Up the Resistance Calculation
To find the resistance, we consider a thin cylindrical shell of radius r and thickness dr. The area dA of this shell is given by:
dA=2πrdr
The resistance dR of this thin shell can be expressed as:
dR=ρdldA
where dl is the length of the cylinder (which we will take as 1 unit length for resistance per unit length calculation).
Step 3: Substituting the Values
Substituting the expressions for ρ and dA into the resistance formula:
dR=cr2⋅12πrdr=c2πr3dr
Step 4: Integrating to Find Total Resistance
To find the total resistance R of the conductor from r=0 to r=a, we integrate:
R=∫a0dR=∫a0c2πr3dr
Calculating the integral:
R=c2π∫a01r3dr
The integral of 1r3 is:
∫1r3dr=−12r2
Evaluating the definite integral:
R=c2π(−12r2)a0=c2π(−12a2+limr→0(−12r2))
As r approaches 0, the term −12r2 diverges, indicating that the resistance tends to infinity due to the singularity at r=0. However, for practical purposes, we consider the resistance per unit length as:
R=c2πa2
Step 5: Finding the Electric Field Strength
Now, we can find the electric field strength E that causes a current I to flow through the conductor. Using Ohm's law:
E=VL=I⋅R
Substituting R:
E=I⋅c2πa2
Final Results
Thus, the resistance per unit length of the conductor is:
R=c2πa2
And the electric field strength E is:
E=Ic2πa2
We have a long cylindrical conductor with a radius a and a cross-sectional area A. The resistivity ρ of the material is given by:
ρ=cr2
where c is a constant and r is the distance from the axis of the cylinder.
To find the resistance, we consider a thin cylindrical shell of radius r and thickness dr. The area dA of this shell is given by:
dA=2πrdr
The resistance dR of this thin shell can be expressed as:
dR=ρdldA
where dl is the length of the cylinder (which we will take as 1 unit length for resistance per unit length calculation).
Substituting the expressions for ρ and dA into the resistance formula:
dR=cr2⋅12πrdr=c2πr3dr
To find the total resistance R of the conductor from r=0 to r=a, we integrate:
R=∫a0dR=∫a0c2πr3dr
Calculating the integral:
R=c2π∫a01r3dr
The integral of 1r3 is:
∫1r3dr=−12r2
Evaluating the definite integral:
R=c2π(−12r2)a0=c2π(−12a2+limr→0(−12r2))
As r approaches 0, the term −12r2 diverges, indicating that the resistance tends to infinity due to the singularity at r=0. However, for practical purposes, we consider the resistance per unit length as:
R=c2πa2
Now, we can find the electric field strength E that causes a current I to flow through the conductor. Using Ohm's law:
E=VL=I⋅R
Substituting R:
E=I⋅c2πa2
Thus, the resistance per unit length of the conductor is:
R=c2πa2
And the electric field strength E is:
E=Ic2πa2
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
A long round conductor to cross-sectional area S is made of material whose resistivity depends only on a distance r from the axis of the conductor as ρ=α/r4, where α is a constant. Find :
(a) the resistance per unit length of such a conductor,
(b) the electric field strength in the conductor due to which a current I flow though it.
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View Solution
Knowledge Check
A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
AπklA2B2πklA2CπklADNoneA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
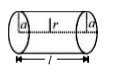 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπThe magnetic field B due to a straight conductor of uniform cross-section of radius 'a' and carrying a steady current varies with the distance 'r' from the centre of conductor as shown in graph .
A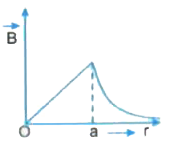 B
B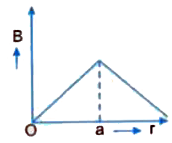 C
C D
D
Two cylindrical conductors with equal cross-sections and different resistivites ρ1 and ρ2 are point end to end. Find the charge at the boundary of the conduction if a current I flows from conductor 1 to conductor 2
View SolutionA cylindrical conductor of length l and radius a has conductivity near its axis as σ. The conductivity of material increases linearly with the distance from axis and becomes 2σ near the surface.The resistance of conductor for longitudinal current is
View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) r<a and (ii) r>a.
View SolutionA cylindrical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
View SolutionA cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
View Solution

