A battery has an emf E and internal resistance r. A variable resistance R is connected across the terminals of the battery. Find the value of R such that (a) the current in the circuit id maximum (b) the potential difference across the terminals is maximum.
Current in the circuit, I=ER+r
Power deliverd to the resistance R is,
P=I2×R=E2R(R+r)2
Power delivered to the load will be maximum when R(R+r)2 is maximum, i.e.,
ddR[R(R+r)−2]=0
or [(R+r)−2+R(−2)(R+r)−3]=0
or (R+r)−3[r+R]=0
As (R+r)−3≠0 for finite value of R,
So, r-R =0 or R=r
When R = r, the power transferred to the load is
=E2r(r+r)2=E24r=max.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Shown n batteries connected to form a circuit. The resistances denote the internal resistances of the batteries which are related to the emf's as ri=k(ε)iwhere K is a constant. The solid dots represent the terminals of the batteries. Find (a)the current through the circuit and (b) the potential difference between the terminals of the ith battery.
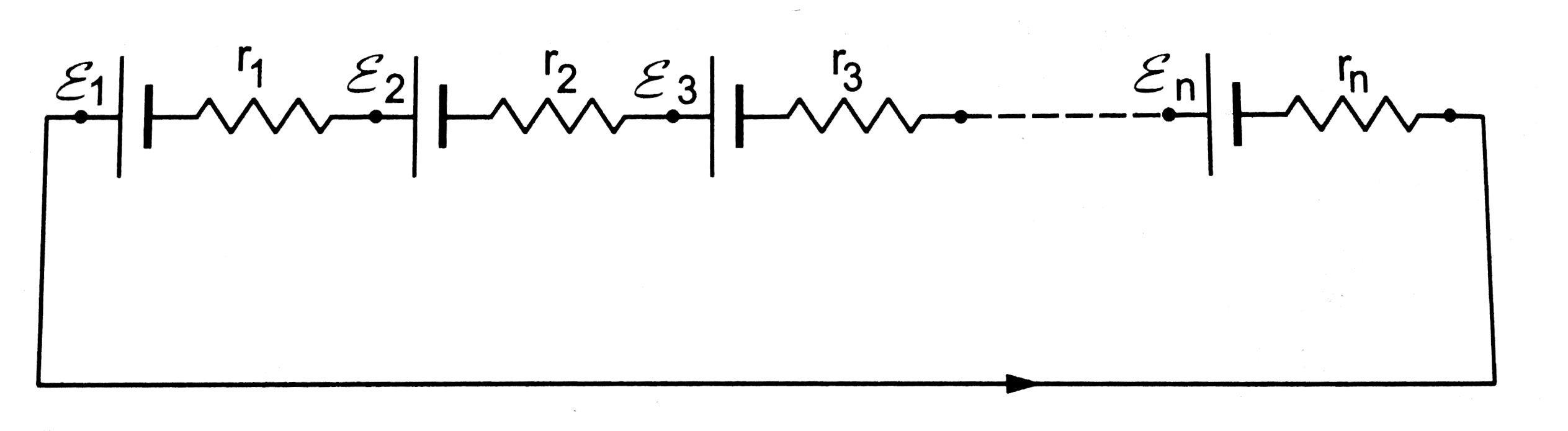
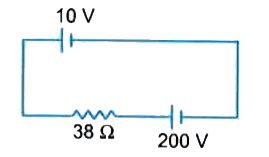
View SolutionA 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38 Ω as shown in the Fig. Find the value of the current in circuit.
View Solution
Knowledge Check
A battery is of emt E and internal resistance r. The value of external resistance R so that the power across eternal resistance is maximum :
ARB2RCR/2DR/4A battery of emf E has an internal resistance r. A variable resistacne R is connected to the terminals of the battery. A current i is drawn from the battery. V is the terminal potential difference. If R alone is gradually reduced to zero, which of the following best describes i and V?
Ai approaches zero, V approaches EBi approaches Er, V approaches zeroCi approaches Er, V approaches EDi approaches infinity, Er, V approaches EA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
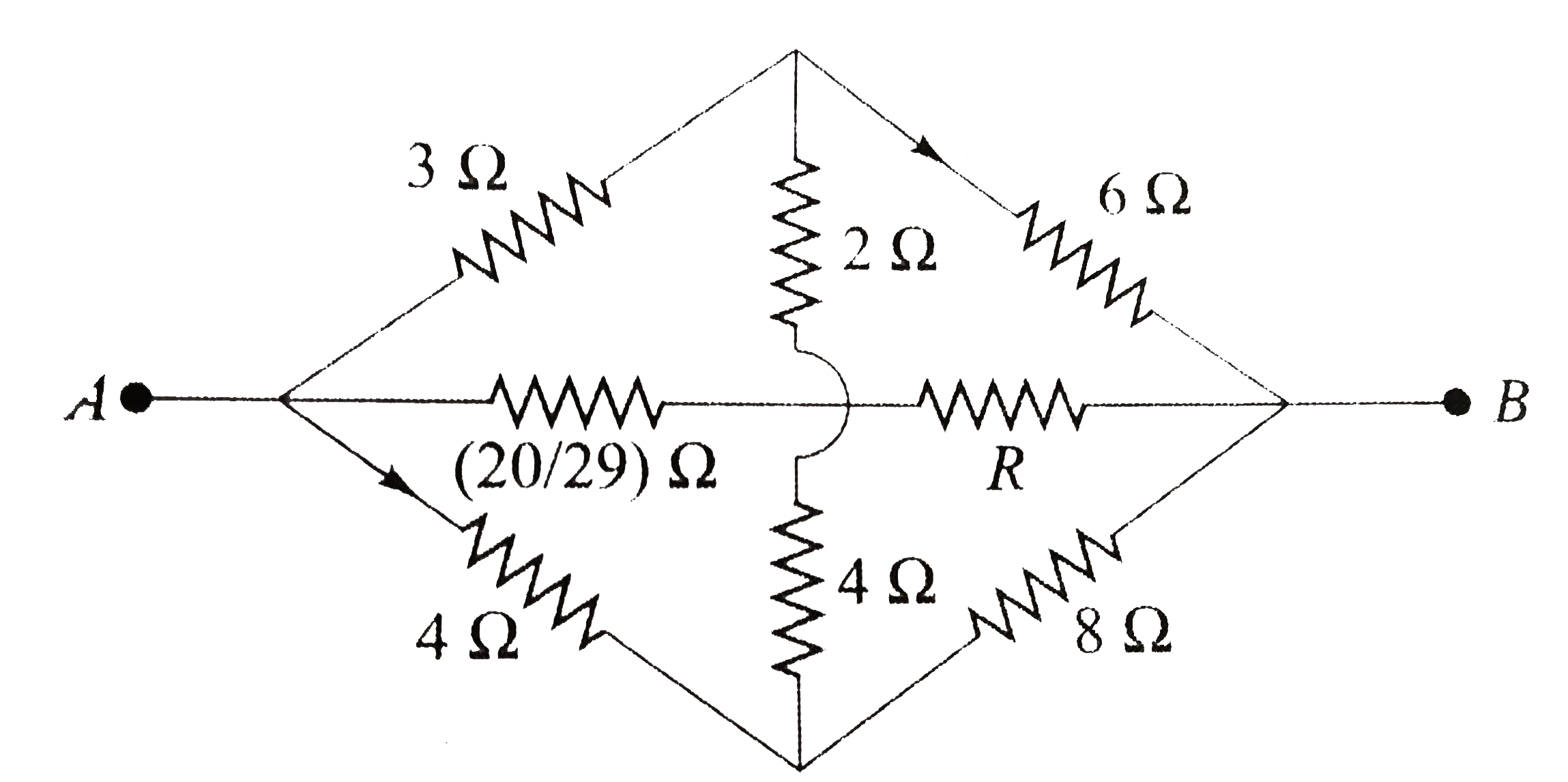 . AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
. AThermal power generated in the external circuit will be maximum possible when R=16/25Ω.BMaximum possible thermal power generated in the external circuit is equal to 4 W.CRatio of current through 3Ω to that through 8Ω is independent of R.DNone of above.
A battery of emf E and internal resistance r is connected to a variable resistor R as shown in figure. Which one of the following is true ?

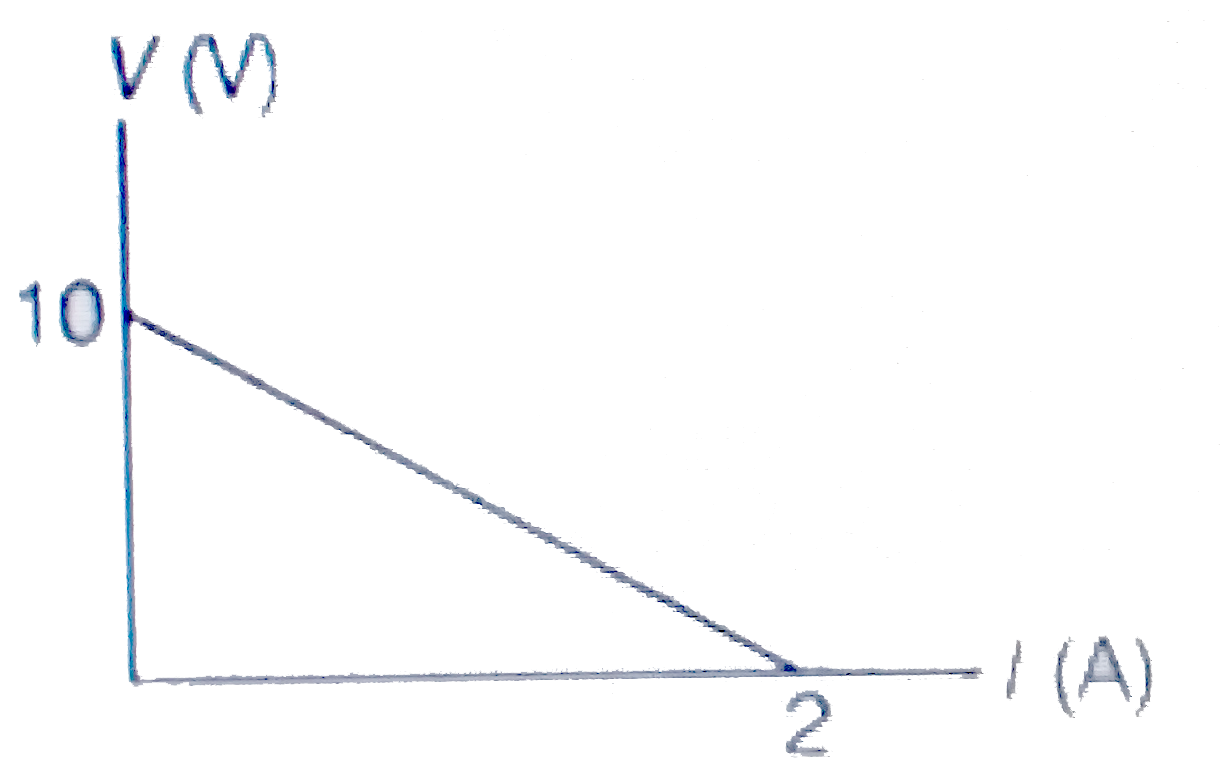
View SolutionA battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference across the termainals of the battery (V). Maximum power developed across the resistance R is
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionCell A has emf 2 E ad internal resistance 4 r. Cell B has emf E and internal resistance r. The negative of A is connected to the positive of B and a load resistance of R is connected across the battery formed. If the terminal potential difference across A is zero, then R is equal to
View SolutionA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View Solution