A battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
2.0ohm
0.25ohm
1.0ohm
0.5ohm
The correct Answer is:D
To solve the problem, we need to determine the value of the variable resistance R for which the power delivered in it is maximum when connected to a battery with an e.m.f. of 10V and an internal resistance of 0.5Ω.
1. Understand the Circuit:
We have a battery with an e.m.f. E=10V and an internal resistance r=0.5Ω. The battery is connected to a variable external resistance R.
2. Power Delivered to the Load:
The power P delivered to the external resistance R can be expressed using the formula:
P=I2R
where I is the current flowing through the circuit.
3. Calculate the Current:
The total resistance in the circuit is R+r. According to Ohm's law, the current I can be calculated as:
I=ER+r=10R+0.5
4. Substituting Current into Power Formula:
Now, substituting I into the power equation gives:
P=(10R+0.5)2R
Simplifying this, we get:
P=100R(R+0.5)2
5. Finding Maximum Power:
To find the value of R that maximizes power P, we can use the condition from the maximum power transfer theorem, which states that maximum power is delivered when the internal resistance r is equal to the external resistance R:
R=r
6. Substituting the Internal Resistance:
Given that r=0.5Ω, we find:
R=0.5Ω
Final Answer:
The value of R for which the power delivered in it is maximum is 0.5Ω.
---
We have a battery with an e.m.f. E=10V and an internal resistance r=0.5Ω. The battery is connected to a variable external resistance R.
The power P delivered to the external resistance R can be expressed using the formula:
P=I2R
where I is the current flowing through the circuit.
The total resistance in the circuit is R+r. According to Ohm's law, the current I can be calculated as:
I=ER+r=10R+0.5
Now, substituting I into the power equation gives:
P=(10R+0.5)2R
Simplifying this, we get:
P=100R(R+0.5)2
To find the value of R that maximizes power P, we can use the condition from the maximum power transfer theorem, which states that maximum power is delivered when the internal resistance r is equal to the external resistance R:
R=r
Given that r=0.5Ω, we find:
R=0.5Ω
The value of R for which the power delivered in it is maximum is 0.5Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section - C
1 Video
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - AIIMS Questions
36 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section B - Assertion Reasoning
28 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
Three equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
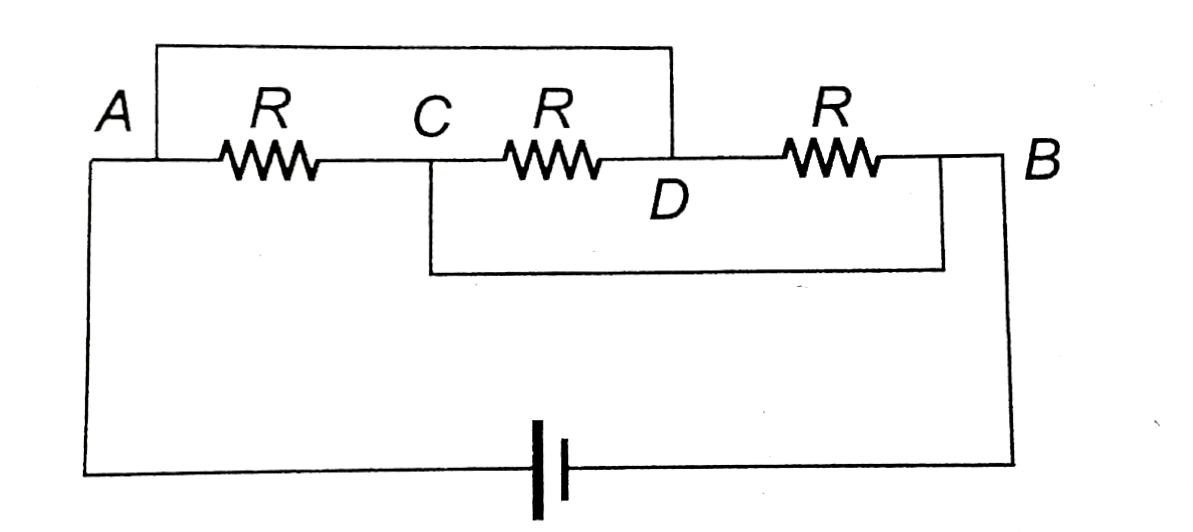 A0.1ΩB0.2ΩC0.3ΩD0.4Ω
A0.1ΩB0.2ΩC0.3ΩD0.4ΩThree equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
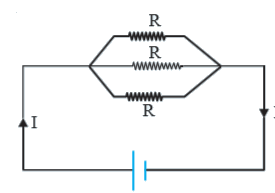 A0.2ΩB0.3ΩC0.4ΩDnone of these
A0.2ΩB0.3ΩC0.4ΩDnone of theseA battery of e.m.f. E and internal resistance r is connected to a variable resistor R as shown here. Which one of the following is true
 APotential difference across the terminal of the battery is maximum when R=rBPower delivered to the resistor is maximum when R=rCCurrent in the circuit is maximum when R=rDCurrent in the circuit is maximum when R>>t
APotential difference across the terminal of the battery is maximum when R=rBPower delivered to the resistor is maximum when R=rCCurrent in the circuit is maximum when R=rDCurrent in the circuit is maximum when R>>t
Three equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
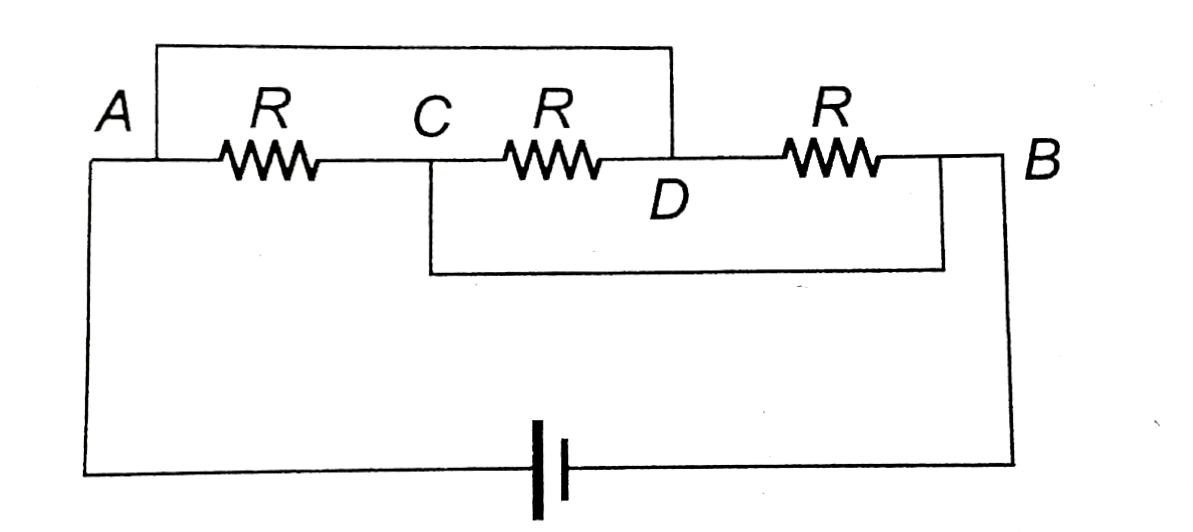
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA battery of emf E and internal resistance r is connected to a variable resistor R as shown in figure. Which one of the following is true ?

View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
View Solution