Resistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
n2R
R/n2
R/n
nR
The correct Answer is:A
To solve the problem, we need to find the equivalent resistance when n resistors, each of resistance rohm, are connected in series, given that their equivalent resistance when connected in parallel is Rohm.
1. Understanding Parallel Resistance:
The formula for the equivalent resistance R of n resistors each of resistance r connected in parallel is given by:
1R=1r+1r+…+1r(n times)
This can be simplified to:
1R=nr
Therefore, we can express R as:
R=rn
2. Finding Individual Resistance:
From the equation above, we can rearrange it to find r:
r=nR
3. Understanding Series Resistance:
When the same n resistors are connected in series, the equivalent resistance Req is simply the sum of all individual resistances:
Req=r+r+…+r(n times)=n×r
4. Substituting the Value of r:
Now, substituting the value of r from step 2 into the series resistance formula:
Req=n×(nR)=n2R
5. Final Result:
Thus, the equivalent resistance when the resistors are connected in series is:
Req=n2R
Conclusion:
The equivalent resistance when the resistors are connected in series is n2R.
The formula for the equivalent resistance R of n resistors each of resistance r connected in parallel is given by:
1R=1r+1r+…+1r(n times)
This can be simplified to:
1R=nr
Therefore, we can express R as:
R=rn
From the equation above, we can rearrange it to find r:
r=nR
When the same n resistors are connected in series, the equivalent resistance Req is simply the sum of all individual resistances:
Req=r+r+…+r(n times)=n×r
Now, substituting the value of r from step 2 into the series resistance formula:
Req=n×(nR)=n2R
Thus, the equivalent resistance when the resistors are connected in series is:
Req=n2R
The equivalent resistance when the resistors are connected in series is n2R.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section - C
1 Video
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - AIIMS Questions
36 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section B - Assertion Reasoning
28 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
If 3 resistances of 3 ohm each are connected in parallel, what will be their total resistance?
View SolutionThe resultant resistance of n wires each of resistance r ohms is R, when they are connected in parallel. When these n resistances are connected in series, the resultant resistance will be
View Solution
Knowledge Check
Equivalent resistance (in ohm) of the given network is
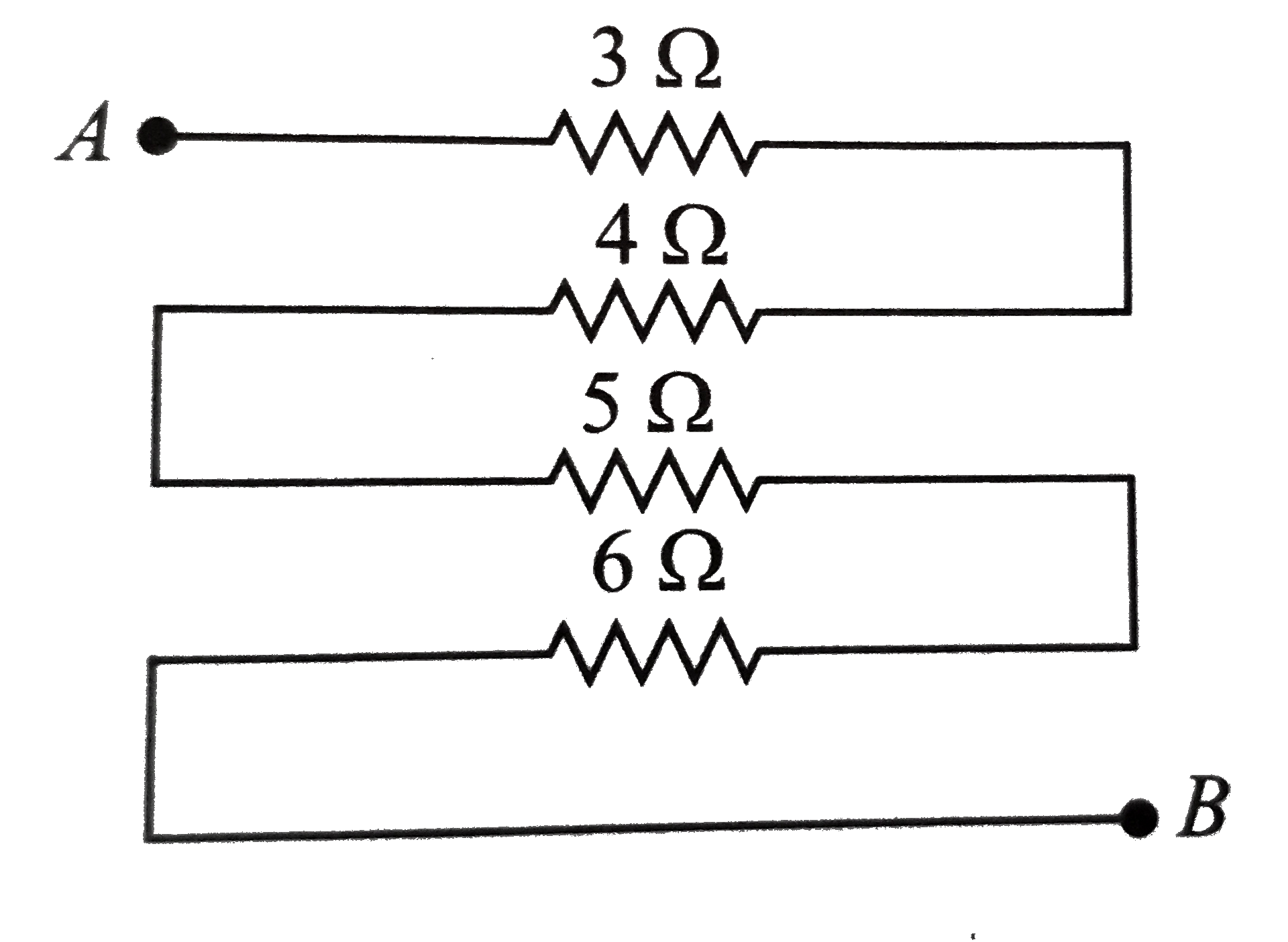 A28B18C26D25
A28B18C26D25A resistance R2 is connected in parallel with a resistance R1 what resistance R3 must be connected in series with the combination of R1andR2 so that the equivalent resistance is equal to the resistance R1 -
AR21R1+R2B(R1+R2)2R1CR22R1+R2DR21R2Three resistors with magnitudes 2,4 and 8 ohm are connected in parallel. The equivalent resistance of the system would be
Aless than 2 ohmBmore than 2 ohm but less than 4 ohmC4 ohmD14 ohm
Two resistances when connected in parallel give resultant value of 2 ohm, when connected in series the value becomes 9 ohm. Calculate the value of each resistance.
View SolutionTwo resistances when connected in parallel give resultant value of 2 ohm, when connected series the value becomes 9 ohm. Calculate the value of each resistance.
View SolutionIf four resistance, each of value 1 ohm, are connected in series, what will be the resultant resistance?
View SolutionThe equivalent resistance of three equal resistances connected in series is 27Ω. There equivalent resistance when connected in parallel is
View SolutionR is the equivalent resistance of n resistors of same resistance in series. If the connection is turned parallel then equivalent resistance will be:
View Solution