A parallel plate capacitor of 300μF is charged to 200V. If the distance between its plate is halved, what will be the potential difference between the plates and what will be the change in stored energy ?
The correct Answer is:100V,3J
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the initial charge on the capacitor
The formula for charge Q on a capacitor is given by:
Q=C⋅V
where:
- C=300μF=300×10−6F
- V=200V
Substituting the values:
Q=300×10−6F×200V=6×10−2C
Step 2: Determine the new capacitance after halving the distance
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
When the distance d between the plates is halved, the new capacitance C′ becomes:
C′=ε0Ad/2=2⋅ε0Ad=2C
Thus,
C′=2×300μF=600μF
Step 3: Calculate the new potential difference
The charge Q remains the same when the distance is halved. The new potential difference V′ can be calculated using:
V′=QC′
Substituting the values:
V′=6×10−2C600×10−6F=6×10−2600×10−6=100V
Step 4: Calculate the initial energy stored in the capacitor
The energy U stored in a capacitor is given by:
U=12CV2
Calculating the initial energy U1:
U1=12×300×10−6F×(200V)2
U1=12×300×10−6×40000=6J
Step 5: Calculate the new energy stored in the capacitor
Now, calculate the new energy U2 with the new capacitance and potential difference:
U2=12C′(V′)2
Substituting the values:
U2=12×600×10−6F×(100V)2
U2=12×600×10−6×10000=3J
Step 6: Calculate the change in stored energy
The change in stored energy ΔU is given by:
ΔU=U1−U2
Substituting the values:
ΔU=6J−3J=3J
Final Results
- The new potential difference between the plates is 100V.
- The change in stored energy is 3J.
The formula for charge Q on a capacitor is given by:
Q=C⋅V
where:
- C=300μF=300×10−6F
- V=200V
Q=300×10−6F×200V=6×10−2C
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
When the distance d between the plates is halved, the new capacitance C′ becomes:
C′=ε0Ad/2=2⋅ε0Ad=2C
Thus,
C′=2×300μF=600μF
The charge Q remains the same when the distance is halved. The new potential difference V′ can be calculated using:
V′=QC′
Substituting the values:
V′=6×10−2C600×10−6F=6×10−2600×10−6=100V
The energy U stored in a capacitor is given by:
U=12CV2
Calculating the initial energy U1:
U1=12×300×10−6F×(200V)2
U1=12×300×10−6×40000=6J
Now, calculate the new energy U2 with the new capacitance and potential difference:
U2=12C′(V′)2
Substituting the values:
U2=12×600×10−6F×(100V)2
U2=12×600×10−6×10000=3J
The change in stored energy ΔU is given by:
ΔU=U1−U2
Substituting the values:
ΔU=6J−3J=3J
- The new potential difference between the plates is 100V.
- The change in stored energy is 3J.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
The plates of a parallel-plate capacior are given equal positive charges .What will be the potential difference between the plates ? What will be the charges on the facing surfaces and on the outer surfaces ?
View SolutionIn a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
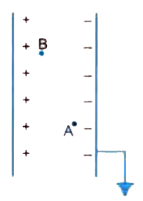
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
Achances of electrical break down will increases if potential difference between the plates is kept constant.Bchance of electrical break down will decreases if potential difference between the plates is kept constant.Cchance of electric break down will increases if charge on the plates is kept constantDchance of electrical break down will decrease if charge on the plate is kept constant.One plate of a capacitor of capacitance 2μF has total charge +10μC and its other plate has total charge +40mUC. The potential difference between the plates is (in Volt).
A7.5B15C25D50The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
ACV22dBC2V22d2CC2V2d2DV2dC
Two parallel plates, separated by 2 mm of air, have a capacitance of 3×10−14μF and are charged to a potential of 200 V. then without touching the plates, they are moved apart till the separation is 6 mm. (i) what is the potential differene between the plates ? (ii) what is the change in energy?
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe capacitance of a parallel plate capacitor is 12μF. If the distance between the plates is doubled and area is halved, then new capacitance will be
View SolutionThe plates of a parallel plate capacitor are charged to 100V. Then a 4mm thick dielectric slab is inserted between the plates and then to obtain the original potential difference , the distance between the system plates is increased by 2.00 mm. the dielectric constant of the slab is
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View Solution